I have my issues with "ideal" models, they are useful but rarely "perfect. So when an "ideal" model/concept is used in a number steps during a derivation, I always look for how wrong can that be. I may be a bit of a pessimist, but that is something I consider "normal" because virtually nothing is absolutely 100% efficient. The Gravito-Thermal "Effect" seems to boil down to interpretation of an ideal kinetic temperature concept used to formulate the ideal gas laws.
Hyper-Physics has a very nice explanation of Kinetic Theory.
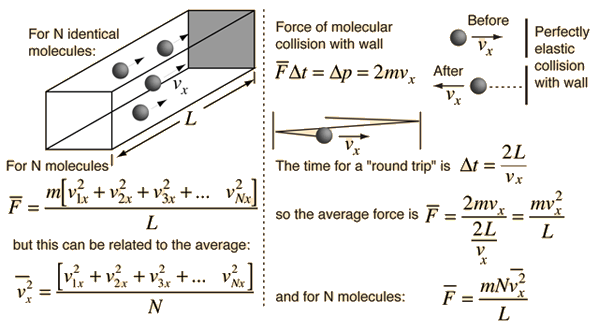
The force exerted by any number of gas molecules can be simplified by assuming "perfectly" elastic collisions with the walls of a container, ignoring collisions with other molecules, so that kinetic energy is *exactly* equal to;
If you include gravity, the force exerted upwardly would always be less than the force exerted downward. When you have a lot of molecules and a small distance between top and bottom, the difference is negligible. The greater the distance, the more likely there will be some significant difference in the force applied to the top and bottom of the "container" which is the Gravito-Thermal effect. If you have a scuba tank, don't expect to see any temperature difference. If you have a very tall tank with very few molecules, there is a likelihood there will be some "kinetic temperature" difference between the top and bottom. Kinetic temperature is in quotes because what it really is is average applied force. That is the very first assumption made in the derivation.
So if you install a pressure sensing plate, like a thermocouple at the bottom and top of a very tall container they would measure different applied pressures even though everything else in the container remains constant.
Remember though that Kinetic or translation temperature doesn't include anything but three directional degrees of motion or freedom. Real molecules have more tricks up their sleeve that can produce radiant energy transfer and stored energy as in potential or enthalpy. The ideal gas concept promotes conduction which is related to diffusion in a gas, to the grandest of poobahs of heat transfer. In the real world conduction is gases is pretty slow and not all that efficient.
Most folks would drop the subject about now and admit that there would be a "real" temperature difference in some cases, but there are so many other "real" issues that have to be considered that any further discussion of the Gravito-Thermal effect based on an ideal gas is about the largest waste of time imaginable. Not so in the world of academia where every nit is a potential battle ground.
Key points for them wishing to waste their time would be is gravity an "ideal" containment since gravity doesn't produce heat, it is the sudden stops that produce the heat. If the gas has the "potential" to whack something and doesn't, it doesn't transfer an force so it is not producing the heat which would be the temperature in the case of an ideal gas.
Some of the more creative seem to think this "ideal" case will result in a fantastic free energy source that will save the world. I am not sure why "saving the world" always seems to boil down to the more hair-brained of concepts, but that does appear to be the tendency. A neutron busting the hell out of a molecule produces much more energy which has a proven track record of providing usable energy when properly contained and not embellished with Hollywood fantasy super powers. But as always, one persons dream is another's nightmare. Even if all the fantasy inventions worked, there would still be a need for someone to save the world from perfection.
During the last "debate" I mentioned that for a rotating planet, the maximum velocity of the molecules in the upper atmosphere would be limit by the escape velocity or speed. So even ignoring all the other minor details, gravity has containment limits which would be temperature limits. Earth for example loses around 3 kilograms per second of hydrogen in spite of having a geomagnetic shield that helps reduce erosion of the atmosphere and there are molecules somewhat suspended in pseudo-orbits of various duration depending on their centrifugal force versus gravitational force. Centrifugal and gravitational forces again don't produce heat until that energy is transferred. So a cluster of molecules could be traveling along at near light speed, minding their own business, having a "local" temperature that would tend to change abruptly if the clusters whacks another cluster. Potential energy is not something to be ignored.
Speaking of potential energy, during the last very long discussion, the Virial Theorem made a showing and I was chastised for mentioning that the VT produces a reasonable estimate. This lead to another *exact* discussion where if you force the universe to match the "ideal" assumption required, mathematically, the "solution" is *exact*. Perfection doesn't really exist sports fans. Every rule has its exception which is what makes physics phun. In "ideal" cases those constants of integration are really constants but in the real world they are more likely complex functions. More often than not, assuming the constant is really constant is close enough for government work, but a smart engineer always allows for a bit of "slop" or inefficiency if you prefer. Some scientist tend to forget that, so IMHO, it is always nice to have an engineer on hand to provide reality checks.
What was interesting to me about the whole discussion was how the universe tends to prefer certain version of randomness more than others. For the Virial Theorem, T=2*Tp or kinetic energy is equal to 2 times the potential energy. So Total Energy is never equal to a perfectly isothermal of maximum entropy state. Since the universe is supposed to be moving towards an ultimate heat death or true maximum entropy some billions and billions of years in the future, potential energy should slow be reducing over time. That would make the Virial Theorem a good estimate for the way things are now which should be close enough for a few billion generations. So for now, potential is about 2/3 of total so the things physical in the universe should prefer a ratio in the ballpark of 1.5 to 2.
If you have read some of my older posts, V. M. Selvam likes to use the Golden Ratio of ~1.618... in her Self Organizing Criticality analysis and Tsallis among others finds similar common ratios for "stable" systems. Nothing is required to be "stable" in dynamics forever so "preferred state" is probably a better term than "stable state". When things get close to "equilibrium" 2nd and 3rd order influences can tend to ruin that "equilibrium" concept which is joined at the hip with the entropy concepts.
Boltzmann's concept of entropy would then be a bit too ideal, which started the whole Gravito-Thermal debate to begin with. Gibbs, Tsallis and many others have functions, intentional or not included in their definitions of entropy to allow for the "strangeness" of nature. Nature probably isn't strange at all, our ideal concepts are likely the strangeness, which is apparent in any debate over the Gravito-Thermal Effect.
Update: Since I started this mess I may as well link to John Baez and his Can Gravity Decrease Entropy post. He goes into more detail on the Virial Theorem on another post in case you are curious. The main points, IMHO, is that a gravitationally bound system cannot ever really be in "equilibrium". with its surrounds and the basic requirement for an isothermal or even an adiabatic system is the need for some "real" equilibrium. Boltzmann's entropy is a attempt to maximize "within a volume", that f=ma issue and a system bounded by gravity is trying to increase entropy by decreasing potential energy, i.e. compressing everything to create heat/kinetic energy. A gravitationally bound system will either completely collapse or portions will boil off. The Ideal kinetic model maximizes entropy by not allowing anything to boil off.
.
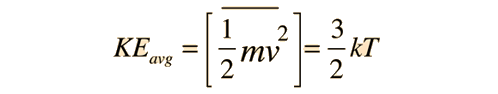
No comments:
Post a Comment