Dragon Kings and Swans of Another Color

That chart is of the Hadley Climate Research Unit (HADCRU) Sea Surface Temperature (SST) version 2, HADSST2 which just for grins I converted into energy, Watts per meter squared Wm-2 because I am working on a model for the climate.  Not a particularly fancy model, just a simple energy balance model.  I included the curved lines to illustrate the approach to an equilibrium energy level.  The spike at the start of the orange portion of the plot is the 1998 Super El Nino.  The orange decay curve that I included is a little exaggerated, but it was not intended to be an attempt to determine a rate of decay, just illustrate that it should be decaying to the common energy of approximately 425.7 Wm-2 or so.

This is the same chart with the RSS global stratosphere temperature in red.  The scales are different, I just added the stratosphere data to show the shift around 1995 to 1996 that tends to agree with the flattening of the HADSST2 prior to the 1998 El Nino.

This flattening is generally believed to be the result of the Pinatubo volcanic eruption.  That is possible, I am more inclined to believe it is due to the upper layer of the oceans reaching what would be their normal energy content.  The 20th century started under somewhat cooler than normal circumstances, rose to near normal in 1945, then there was an unusual drop in SST that is largely unexplained.  Typically, I could give a rat's butt what climate science is doing, but since there are unexplained things and overly confident scientists saying that we all need to give until it hurts because of Global Warming, I have done a little looking and this is not something that any of the best and brightest of climate science has taken note of recently.  If fact, many seem to avoid this like the plague.  It does not fit climate theory.

Since I am not a conspiracy theorist, I will give climate scientists the benefit of the doubt and just assume they are idiots.  Since the idiots, er climate scientists, are predicting doom in the next 100 years or so, including a "black swan" event in the next decade, I thought I would get my prediction in as well.

A "dragon king" is a completely unpredictable event and a black swan is an unexpected, but should have been predictable event.  I am saying that the 1995 shift to neutral warming of the oceans was a dragon king that sets the stage for a major series of black swans that the climate scientists will call a dragon king because they never realized that the dragon king had already happened, it was just waiting for the right push.  So this "Dragon King" which will make the headlines in the next few years to a decade, should have been just a black swan if the climate scientists had any real clue what they were doing.

So I am predicting two Dragon King events, the first a major cooling period during the next solar minimum and the second the complete loss of faith in climate science because they should have known but didn't.  A teens twofer.  Later this year, the fifth IPCC report will be produced.  There will be plenty of fresh climate predictions just in time for climate reality to set in.

So this is just to make my prediction public.  Enjoy the laughs at how foolish it is.  We'll check back in a decade to see how poorly someone did.

Follow the Energy

Figuring out stuff is pretty easy.  Explaining it can be the real bitch.  It is easier some times to let people find their own starting point to figure things out for themselves.  Look at the boxes.  Let 32C be constant and -1.9C be constant.  How much energy would it take for both to remain constant?  Where would excess energy go?



Hint:  The enthalpy of fusion is 334Joules/gram.  The energy of an object at 4C, 277.15K is 5.67e-8*277.15^4=334.5Wm-2, a Watt per second is equal to a Joule per sec.

Why 21.1C?  There are approximately 4.2Joules per gram required to raise the temperature of water 1 degree centigrade.  21.1-(-1.9)=23C 23C times 4.2=96.6Joules per gram.  96.6Joules per gram plus 334=430.6 Joules per gram, balanced by 334+4.2*(21.1-0)=422.6 Joules per gram.  (430.6+422.6)/2=426.1Joules per gram for fresh water.  The equivalent energy of an object emitting 426.1Joules/second is 294.5K degrees or 21.35C.  Why 21.35C and not 21.1C?  An object at a temperature of 21.1C, 294.25K would emit 425.06Joules per second if it were a perfect black body.  Water emits 425.06/426.1=0.99756 or 99.756% of a perfect black body.  Plus or minus a schoosh, determine the more exact changes in specific enthalpy per degree and you should arrive at the emissivity of salt water.

Why 425.06Wm-2 and not 390+/- the average surface energy?  The atmospheric window allows approximately 35.4Wm-2 to leave the surface without impacting the atmosphere.  425.06-35.4=389.7 Wm-2.  From the heat of fusion, 334Joules per gram plus 23.52, the enthalpy required to change water at 4C to -1.9C, equals 357.52.  Add the 35.4 joules per second energy not interactive and 392.92 Wm-2.  Again use the more exact values for properties of salt water and fresh water, and you will arrive at a more precise estimate of the surface energy in equilibrium.

CO2 and other radiant gases appear to impact the 35.4Wm-2 atmospheric window which varies to maintain the ice, liquid ocean and moist air enthalpy balance.  A very interesting system of feed backs.

Maximum Entropy and the Moisture Boundary Layer Model

Using the Moisture Boundary Layer (MBL) model with a fixed lower temperature limit of -1.9C and the approximate average Sea Surface Temperature (SST) of 21.1 C there are a few things that can be inferred but not verified.

With the average radiant energy of 306.9Wm-2 at the top of the MBL and an average measure energy out for the Top of the Atmosphere (TOA) of 239Wm-2, the average radiant energy of all surfaces above or outside of the MBL envelope would be 306.9-239=67.9Wm-2.  

By assuming maximum entropy equals 50%, a radiant boundary layer can be approximated at 306.9*0.50=153.4Wm-2.  Using the same maximum entropy assumption, a second boundary at 153.4*.5=76.6Wm-2.  Ideally, this second boundary would be equal to the first estimate of 67.9Wm-2, there is uncertainty in all of the estimates though.  One of the larger uncertainties is the absorption of energy, solar and outgoing long wave, in the atmosphere, another is the energy that gets a free pass through the atmospheric window.  So maybe there is another way of looking at the problem?

A second way would be that while the surface is radiating 425Wm-2 inside the MBL, only 118.1Wm-2 is lost at the -1.9C boundary (306.9Wm-2), leaving 188.8Wm-2 (425-306.9Wm-2) unaccounted for in the 50% maximum entropy estimate.  50% of the 188.8Wm-2 would be 94.4Wm-2.  This would be the total energy absorbed by the atmosphere from the surface and the sun.  That results in to competing choices for the more appropriate radiant boundary layer, 188.8 for the MBLtotal and 153.4 for the MBL outer envelope.  Without trying to over complicate this analysis, 188.8-153.4=35.4Wm-2 should be energy that is not doing anything or the "effective" atmospheric window radiation from the MBL.  Proving that may be a challenge :)

With an ever so rough estimate of the atmospheric window radiation, 35.4Wm-2, we may be able to work back to isolate the where and what's.  By reducing both the MBL surface and outer boundary by 35.4, we get an "effective" surface of 425-35.4=389.6Wm-2 and 306.9-35.4=271.5Wm-2, the difference would be 389.6-271.5=118.1Wm-2 so the MBL energy is still intact, 271.5-35.4=236.1 which is in the ballpark of the TOA emissivity.  This implies that MAXENT needs a 35.4Wm-2 fudge factor.  Not a permanent fudge, just one to carry until we know where to stick it :)

With the TOA flux at 236.1Wm-2 and assuming the 35.4 is free pass we can use maximum entropy and work backwards again.  236.1-25.4=200.7, 2*200.7=401.4Wm-2 which would be the perfect maximum entropy surface radiant energy if there were no tropopause or energy absorbed in the atmosphere above the surface of course neglecting our PITA free pass energy.  Which should be the maximum average surface energy of the planet unless the free pass window closes somewhat.  With Ein=Eout at the TOA required, we have a near ideal 200.7 as a greenhouse effect, 306.9-236.1=70.8 as the GHE using the MBL as a surface and the 35.4 PITA free pass.  That should make the radiant interaction or OLR absorbed by the atmosphere  approximately 70.8-35.4=35.4Wm-2 which implies there may be no free pass radiant window from the true surface but from an average radiant layer inside the MBL, like cloud tops.

I am posting this just in case anyone is following.  The object is to have a moist air boundary model and a maximum entropy model which together should highlight any screw ups in each other and provide some sense of confidence as long as they agree, only not perfectly.  Where they disagree should be on conductive impacts or sensible if you prefer.

How to Bound an Open System

Carnot Engine from Wikipedia

For some reason the simplest principles of thermodynamics baffle people.  In any engine, there is all sorts of stuff going on inside.  What matters most is what comes out compared to what goes in.  Nicholas Leonard Sadi Carnot was a French Military Engineer that knew that.  To simplify a problem he developed the Carnot Engine.  That simple drawing was too complicated for some to understand so it was simplified even more.

The Qn is the energy in, Qc is the energy out and W is the work.  So Qh=Qc+W,  If Qc=W, then only half of the energy is converted into usable work.  Only half is pretty damn good really, your car engine is only about 0.35Qh.  A modern gas turbine engine is close to 0.45Qc and if you add a cogeneration process like a steam turbine that uses the some of the 0.55Qh which is Qc, you can get more work, kicking the entire process up to 0.6Qh, or 60 percent efficiency.

Two Stage Carnot Heat Engine

You can never get all the good out of Qh because of entropy, typically noted with the letter S.  There is no perfect engine.  With that in mind, any thermodynamic process can be simplified to some combination of Carnot Heat Engines, even the Earth's Atmosphere.

Atmosphere as a Carnot Heat Engine

As all Red Neck Theoretical Physicists know the best place to start is at the beginning.  For maximum entropy, W=Qc=S for each process and  the whole process.  If it doesn't, try to figure out why.

Atmosphere as a Carnot Heat Engine and some Initial Values to Play with

Play with this simple model of a complex Atmospheric/Ocean system a see what you think, Physics is Phun!

The Faint Young Sun and Liquid Water is not a Paradox

Carl Sagan proposed the faint young paradox, where liquid water could not exist on Earth with the faint young sun having an energy output of only 70% of what it is today.  This is not only not a paradox, but an illustration of the lack of understanding of thermodynamic in astrophysics circles.

With the current average solar radiation at the top of Earth's atmosphere determined to be 1360.8Wm-2, the faint young sun energy would have been .7*1360.8=952.6Wm-2.  Felt at the surface of the ocean, that 952.6Wm-2 is capable of raising the specific heat of water by 952.6 Joules per gram.  With the specific heat of water being 4.2Joules/gram per degree C, 952.6/4.2=226.8 increase in temperature per gram of water at the surface skin layer.   To illustrate, consider a cubic meter of water equal to 1 million layers of one gram of water each, i.e. there are 1000kilograms of water per cubic meter with the density of water being 1kilogram per liter.  There are 1000 gram per liter or kilogram, one cubic meter of water has a mass of 1000 kilograms.  Applying  heat at a rate of 952.6Wm-2 per second for a period of one hour would increase the energy of the cubic meter of water by 952.6*60*60=3.429,360 Joules or 3.43Joules per gram of water.  For a period of one hour at solar noon.  For a equatorial location, one half of the 952.6Wm-2 would be the average energy applied for a 12 hour day.  952.6*4.2*60*60*12/2=86,419,872 Joules per cubic meter or 86.4 Joules per gram.  The true question is if the energy gained in the day would be lost at night?

The specific heat of dry air is 1.006 Joules per gram more than 4 times lower than the specific heat of water at sea level.  At the surface skin layer, the boundary between the liquid water and the dry air, the water would have to transfer energy to the air and cool.  The paradox is that the surface skin layer would also radiate to space.  Unlimited, the rate of cooling to both air and space would exceed the rate of warming.

The minimum surface temperature of liquid salt water is -1.9C which has a radiant energy of 307Wm-2.  With an average solar energy applied of 952.6Wm-2/4 the average global energy, the energy in, 238.15Wm-2 which is less than the minimum radiant energy of a liquid water surface.  However, for a tropical location, the average is actually, 952.2/2=476.1Wm-2  Allowing for the true orbital maximum insolation which is higher, the loss of energy for the mass of water gained during day only has to equal  or less than the loss at night.

To set up or faint young sun scenario consider that as ice is formed in salt water, most of the salt is expelled as the ice forms resulting in fresh ice.  The melting point of fresh ice is 1.9 C greater than the freezing point of salt water.  As the salt water warms it would transfer heat to the surrounding fresh ice.  The specific heat of fresh ice is 2.1Joules per gram.  With all sides and the bottom of the cubic meter or liquid salt water enclosed by fresh ice, there would be 2.1*5=10.5 Watts per second transferred to the fresh ice.  As the ice gains energy, it would approach the latent heat of fusion of 334Joules per gram at a temperature of 0 C degrees.  Since the salt water can be at a lower temperature than the temperature of the latent heat of fusion, the energy flow from the salt water to fresh ice would approach zero, providing perfect insulation at this skin layer until either the salt water warmed above -1.9 C or froze, at which point it would have to release 334 Joules per gram.  At equilibrium there would be no heat exchanged between the salt water and the fresh ice.

That leaves the surface exposed to the atmosphere.  As the surface skin layer of the salt water released heat to the air, the specific heat capacity of the air would limit the heat flow.  With a specific heat of 1.006, the conductive flow rate would be equal to 1.006 Watts per meter squared for still air.  The radiant energy of the surface would be 307Wm-2 from the salt water but would have to increase to 316Wm-2 if the skin layer lost enough energy to form ice.  There would again be an insulating effect of fresh ice now on all sides of the cubic meter of salt water.  The rate of heat loss would be limited by the specific heat of fresh ice at -1.9 C degrees.

Our cubic meter of salt water now contains 86,419,872 Joules and on all sides is insulated by fresh ice.  The rate of energy flow from the center of the cube is totally dependent on releasing 334 Watts per meter squared on six sides limited by a temperature difference of 1.9C, the difference between the temperature of the freezing salt and melting fresh ices.  The surrounding ice insulation barrier limits the energy exchange to 2.1*6=12.6Wm-2 per second.  over the course of the night, the salt water would lose, 12.6*60*60*12=544,322 Joules plus 6*334=2004 Joules for the surrounding heat of fusion of the initial skin layer of ice.  At the skin ice layer exposed to the atmosphere, the initial radiant loss would be 316Wm-2 which would decrease as the skin layer cooled at a faster rate that the internal energy could provide.  The radiant energy would decay to 2.01Wm-2.  Assuming that the rate of decay to 2.01 resulted in half the initial emission energy of 316Wm-2, then 316*60*60*12/2=6,825,600 Joules.   The final energy of the cubic meter of salt water would be 86,419,872 Joules minus 6,825,600 Joules radiated minus 544,322 Joules conducted plus 2004 Joules latent heat for the fusion of the initial skin layer resulting in 80,136,590 Joules of retained energy.  So if salt water existed for any reason in the tropics, a faint young sun could maintain the liquid water and expand its area.


From a frozen surface the puzzle is different.  If the albedo of the surface does not allow a minimum of 2 (for the full 24 hours) times 6,825,600 Joules to be absorbed per cubic meter then there would be no liquid water surviving until the next solar noon.  The albedo of clear ice would allow nearly full absorption but for only solar noon plus and minus one to two hours.  At 952.6Wm-2 per second the maximum total energy absorbed per hour would be 952.6*60*60=3,429,360 for full absorption.   Not enough energy would be provided to ensure liquid water at the surface.  Enough energy though to help melt a skin layer of ice form a liquid water starting point.

Depending on the geometry of the pool of liquid water, the volume would expand more rapidly than the surface area.  The boundary of the liquid water would require some minimum energy.  For the liquid water example, 6,825,600Joules is the approximate minimum required to maintain liquid salt water.  That is only an average energy at the surface of 158Wm-2 either by solar or any other means of heat transfer.  That means the faintest faint sun could be 632Wm-2 at the surface if any volume of liquid water existed.

Feel free to review the calculations and the logic, I will review this later myself.

 

Geothermal energy below the surface would be the key for the initial formation of liquid water if a snow ball Earth ever existed.  With the large number of equatorial submarine volcanoes, it is unlikely that a snow ball Earth existed for long if it did at all.

What does Average Global Surface Temperature Mean?

Starting with the majority of the Earth's surface, the oceans. and including the moist air envelope in the atmosphere that results from the liquid of the oceans, you find that the average temperature of the sea surface temperature (SST) is limited to a very tight range of temperatures.  The true average SST would range from 21 C to 22.5C with a rather small margin of error.  The average is limited because the freezing point of fresh and salt water ranges from -1.9C to 0C at surface atmospheric pressures and the rate of evaporation at sea level would have to closely match the rate of freezing if the oceans are to exist.  So how does tight range allow for changes in the Global Average Temperature (GAT)?

If there were no land mass on Earth, the expansion and contraction of ice area would be the impact on the GAT,  With the SST limited to the tight range by the thermodynamic properties of water at sea level, the energy emitted by the sea surface would be fixed at 425Wm-2 +/-20 say, the total energy available from the sun on average is 340Wm-2, so the total energy leaving the Earth would have to be 340Wm-2.  425-340=85Wm-2, so the average energy leaving the non-liquid portion of the Earth's surface and/or atmosphere would have to be 85Wm-2 on average.  No fuss, no muss, 85Wm-2 period end of conversation.  Since the total energy available is 340Wm-2, the non-liquid portion has to emit 85Wm-2, 240-85=155Wm-2, kinda scary right?  That is the Aqua effect, not to be confused with the Greenhouse Effect.  The requirement of conservation of energy, Ein=Eout and conservation of water, the primary thermal mass of the surface, specify very tight limits on the range of possibilities.

As the area of the true liquid sea surface expands, the area of non-liquid surface decreases which requires more reflective surface, clouds in the atmosphere provided by our sponsor, Aqua not so pura, meaning cloud albedo is a required feed back, not an optional feed back. On a true water world with no land mass, the habitable portion of the surface, the not frozen part, would be about 21.5 C plus or minus a touch on average.  The "average" surface temperature would depend on the percentage of cloud cover, but the "average" temperature of the non-liquid surface would range from -76.4C (85Wm-2) to 0C (316Wm-2).

So the "Average" surface temperature is fairly meaningless since only the surface inside of the moist air boundary is critical for the the energy balance.  Any surface at or below -76.4C is not a part of the surface average, but a response to the overall conservation of energy requirement.  Concentrating on the moisture boundary and the relatively minor radiant boundary will prove that the "Faint Sun Paradox", is not a paradox, but a misunderstanding of basis thermodynamics.

Workbench or Bar?

I had a nice visit from code enforcement the other day.  They said that my "work bench" is not allow in plain view.  Evidently "work" is the operative word here, when it was a "bar" it was perfectly allowable.  So I have to keep the tools out of sight or camouflage them with spiced rum labels.    Interesting illustration of perspective.

Astronomers look at a planet and determine by the radiant energy that that planet has a specific temperature.   Eout has to be equal to Ein, so they know every thing they need to know about that planet.  Engineers look at a system and know that Ein is about equal to Eout but there is work going on inside so they peal back the spiced rum label to see what is going on inside.  Energy is fungible, but the work done is not, if the mechanism to perform the work is not there, the work doesn't get done.  So some scientist are more like code enforcement than engineers, they see what they think they see, not what is really there.

Inside where all the good stuff happens tells the tale.  The ocean is a huge mass of water capable of hole huge quantities of energy.  That energy is contained in all directions or the energy would quickly dissipate.  So how is the energy stored, converted and manipulated in the system until it gets to the spice rum label?

Water has a specific heat capacity.  It freezes at a temperature around 0 degrees and boils at a temperature around 100 degrees.  It requires 4.2Joules of energy to raise the temperature of water one degree.  So to change the gram of water from 0 to 100 degrees requires 420Joules of energy plus of minus a touch.

To freeze water, you have to remove 334Joules per gram.  To melt water, you would have to add the 334Joules per gram.  That happens at one temperature for both processes if the water is pure, at two different temperatures if the water is not pure.  Each degree of change in the freezing point to the melting point requires another 4.2Joules per gram of energy.  To evaporate water requires 2257Joules per gram at the boiling point of water which also varies a little depending on the purity.

If the whole range of energy is used from freezing to boiling, a total of approximately 2257+420+334=3011Joules per gram is required.  once the water freezes or evaporates, it is no longer in the ocean, it either floats on the surface or is transferred to the atmosphere. Either way it in no longer in the physical ocean of liquid. If there is no atmosphere the water cannot evaporate and if the water were tightly contained, the container would either expand or burst.  So the volume of water would have to expand or contract if the energy did not remain constant.  For the water cycle, the oceans and atmosphere are fully coupled, meaning a change in one will cause a change in the other.

If I have used the right values this time, the range of temperature for pure water is from 273.15K (0C) to  373.15K (100C) degrees.  Note that 273.16K (0.01C) is more exact, but close enough that I should not have to redo all my drawings :)

The Stefan-Bolztmann Black Body Equation, E=5.67x10^-8(T)^4 is the relationship of the energy emitted by an object at temperature T in degrees Kelvin.   By using the freezing and boiling points of water, the energy range is 1099.3Wm-2 for 100C and 315.6Wm-2 for 0C, a range of 783.6Wm-2 per 100C or 7.84 per degree C.  You may note that this is difference than 4.2Joules per gram where Joules per sec is equal to Watts per second by definition in Systems International units.  Why would that be?

If we had one gram of water spread thinly over a 1 meter square surface between a body of water and space it would emit 7.84Wm-2 outwardly but 4.2Wm-2 inwardly.  It is easier for the energy to flow into space than it is to warm water.  Warmer water has greater potential energy, so the energy of that thin layer of water would do less work and (7.84/4.2=1.86) 86% more escaping.  If the energy flow into the water was equal to the energy flow to space the work done would equal the energy lost, the process would be 50% efficient.  Considering the addition of an atmosphere instead of space, up to 86% more work would be done on the atmosphere than on the water.  The energy is only 14% efficient warming water.

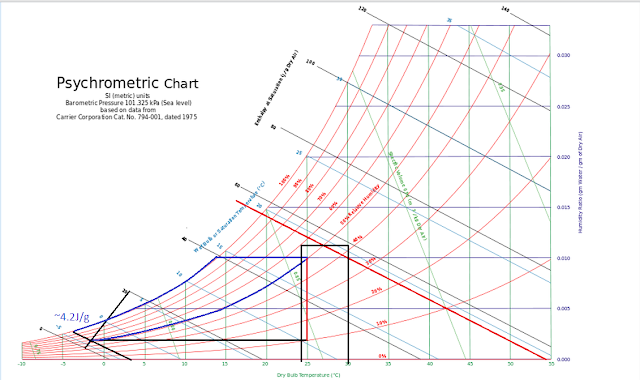
The atmosphere has a specific heat capacity.  1.006Joules per gram of dry air at 25C and 1.013 bars, sea level.  This is close to 1 so to simplify, water has 4.2 times the heat capacity of dry air at sea level and 25 degrees C.  If all of the energy of our thin gram of water was transfer to both the air and water. The air would gain 86 percent more of the 4.2 Joules, .86*4.2=3.16 Joules per gram and .14*4.2=0.59 Joules per gram for water.  Under this steady state condition, it would not take long for all the energy in the water to be lost to the atmosphere.  For equilibrium, the water has to absorb the same energy as the air, water is virtually incompressable and air is not, so the air would have to absorb more energy and expand or more water vapor to increase its specific heat capacity or both.  At sea level, the point were moist air reaches 4.2Joules per gram is approximately -1.9C and 50% relative humidity.  That point varies from approximately -3C for saturated air and to +3C for dry air.

With moisture available because of the ocean and expansion available, limited by gravity, the psychrometric chart provides a reasonable range of conditions inside of the moist air boundary.  The work performed on the atmosphere would be a combination expansion and thermal capacity change.  The work performed on the ocean would be mainly change in the thermal capacity with some limited expansion.  The work performed on each would be equal at equilibrium.

Since we live on a water world, water has been around for perhaps a billion years, there is a pretty good chance that there is some conservation of water involved in the thermodynamics of the system.  There is a pretty good deal of ice on Earth.  We know that ice releases 334joules per gram as it forms so it is somewhat likely that the energy gained would balance energy released.  Using the Wm-2/Joules per second relationship, the maximum energy allowed in equilibrium would be 316Wm-2 plus 334Wm-2 released from the formation of fresh water ice or 650Wm-2 which has an equivalent temperature 327.2degrees K (54.1 degrees C) +/-3 degrees for dry air.   For the water, the energy lost to evaporation would have to be considered.

Since the psych chart is posted above, a simple approximation is just to follow the 50% RH curve until it intersects with the enthalpy of dry air at 54.1C degrees, then add the -3 to +3 range of the lower enthalpy limit.

 As shown, that results in a maximum SST range of 24C to 30C, which is a rough estimate, but generally close enough for government work.  To refine that estimate we can look at the latent heat of evaporation, 2257J/g remembering that we are assuming conservation of the water on the planet.

As ice forms it releases 334J/g of energy.  If that energy is released inside of the moisture boundary, some portion would be transferred to the atmosphere and some to the ocean to regain equilibrium.  When water evaporates it absorbs 2257J/g of energy which is then contained in the atmosphere.  If ice is being formed and evaporation taking place without any reverse of these processes, there would be no liquid water on Earth.  There has to be an equilibrium if liquid water is to be conserved.  When ice is forming and water is condensing, both release energy to the system.  Since the ocean can only absorb 14% of the energy released, 86% would be lost from the system.  If ice melts and water vapor condenses, the system would absorb all that energy, the system would run away.  Over some period of time, the enthalpy released would have to equal the enthalpy gained to conserve both energy and water.  Since the energy of the heat of evaporation is much larger than fusion, it would be the limiting process which can be dealt with by the assumption of a constant relative humidity.  Using the Psych chart we can extent the 50%RH curve to the maximum enthalpy at 54.1C.  Follow that line to saturation, the down the saturation curve to where there is half the initial enthalpy between 4.2J/g, the minimum and approximately 56J/g the maximum, then to the right on the sensible heating line back to 50%RH, that results in an approximate average surface temperature of 21.5C degrees.  Probably close, but enough uncertainty not impress many.

Another way is to consider the energy of the moisture boundary temperature which at 0C would be 316Wm-2.  That energy is provide by the sea surface and only 86% of the sea surface skin layer is transmitted to the atmosphere in equilibrium.  So the effective radiant energy would be 316/.86=367.4Wm-2 or 10.6 degrees C.  That temperature is the saturation temperature on the chart above which when sensibly heated to 50%RH again results in an estimated surface temperature of 21.5C degrees.

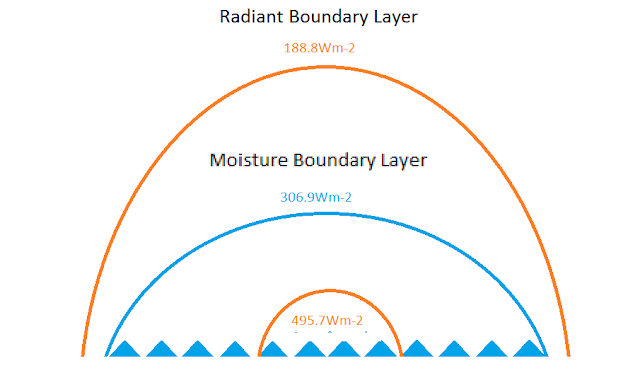
We could even abandon the psych chart and just consider the energy required to balance the heat of fusion of the ice, 334J/g.  Since the ratio of the heats fusion and evaporation is 334/2257=0.1497, only 15% of the mass of ice formed is the needed mass of water evaporated to maintain equilibrium.  So the average surface temperature would be 86% of the distance between the minimum temperature and the maximum temperature.  The maximum temperature is only estimated, so there is a way to estimate the change solely on the 334 J/g, .86*344=287.24Wm-2 plus the initial energy 316Wm-2 would equal 603Wm-2 if the energy was perfectly transferred and contained.  The atmosphere outside of the moisture boundary envelope is far from a perfect container, so energy would be lost in the transfer.  The 603Wm-2 would decrease to equilibrium with the  surface and the moisture boundary envelope at 316Wm-2.  What limit it would decay or reduce to would depend on the energy balancing the 316Wm-2 at the moisture boundary.

This part may be tricky for some.  For the moisture boundary layer to be in equilibrium with space, there must be an equal and opposite balancing force.  50% efficiency is the maximum for this steady state system as mentioned earlier with the 4.2 into the ocean surface versus the 7.84 to space.  At the moisture boundary layer with 316Wm-2 energy, it would be balanced by half with half lost to space.  The 603 would decay by approximately 158Wm-2 to 445Wm-2 if the moisture boundary layer were 316Wm-2.  We have a range of values for the moisture boundary layer though, +/-3C at the boundary.  The point previously plotted on the psych chart at 50% relative was approximate -1.9C which has an equivalent energy of 307Wm-2 which would be balanced by 153.5Wm-2.  For fresh ice to form in a salt ocean it has to release the 334J/g for fusion plus 1.9*4.2=7.98 addition J/g to reduce the temperature by 1.9 C degrees.  The 603 would have to decay an additional 7.98 plus 4.5 or 12.5Wm-2 to 445-12.5=432.5Wm-2 which would have an equivalent temperature of 22.5 C degrees.  The decay would not be perfectly linear nor is the boundary efficiency estimate perfect, but again this should be close enough for government work.

So what does all this BS mean?  Basically, that as long as there is liquid water on Earth with sufficient thermal mass, the ocean average temperature will be in the range of 22.5 C +/- a couple of degrees.  The total area of the open water ocean would vary, the volume of the moist air envelope would vary, but the average temperature of the ocean is surprisingly stable due to the thermal properties of water and moist air.  A point completely glossed over in the global warming debate.

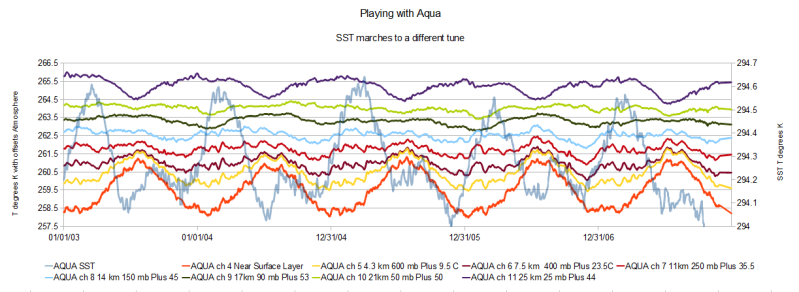
Think of what this simple model projects, a maximum surface temperature of 54.1C, Aziziya, Libya has a maximum record temperature of 57.8C that has never been repeated with the next maximum list as 54C in Israel.  The average SST range via the AQUA satellite is approximately 294.25K degrees 21.1C degrees, 1.4C less than the model estimate that made a linear assumption for an energy decay.  These are actual values compared to a crude model that does not seriously consider any radiant impacts or even mass, volumes or input energy.   Any significant radiant impact from Greenhouse gases will be felt outside of the moisture boundary envelope which will considerably reduce any current estimate based on radiant only impact looking in from the spiced rum sticker :)

I haven't completely proofed this, but since it was raining today, felt like posting a different perspective.

The Not Forth Coming Ice Age

UPDATE: Replaced figure.

Using the simple moisture boundary layer model with the range of salt to fresh freezing point temperatures and assuming that sea surface temperature would maintain a relative constant average, the drawing above is an approximate range of equilibrium states.  Below each reference layer is a temperature range in degrees K or C and at the bottom, the equilibrium temperature estimate for the deepest oceans, the abysmal depths.

The Saltwater baseline has a lower abysmal depth temperature of 2.73C and the Fresh has a higher 4.39C temperature for equilibrium.  True equilibrium is unlikely in a complex dynamic system, so the values are limits not set point.  The Moisture Boundary Layer (MBL) variation is 0.95C above and below the average and the Radiant Boundary Layer is 1.98C to 2.06C above and below the average temperature.  These variations do not indicate what the "Average" global surface temperature range may be because the MBL and RBL envelopes expand and contract with changes in the available energy.  For this example there could be no change in the average sea surface temperature just variations in the area of open water.

While I make no claim that the assumption of a constant average SST is valid, there is reason to believe that the range would be much smaller than the range of any other reference.  The abysmal depths are likely the most stable reference and it agrees fairly well with the model assumptions, but there is not a great deal of data on the ocean depths.  There is plenty of room for tinkering, but the results resemble reality thus far.

Isothermal Boundary Layers

The Moisture Boundary Layer model uses the latent heat of fusion as a reference boundary.  The drawing above shows the MBL in light blue roughly oriented to the actual Earth.  Since the Earth has predominately salt water available in liquid form, the temperature of the MBL would approximately 271.25K degrees (-1.9C) slightly below the freezing point of fresh water.  To simplify calculations, instead of actual temperature, it is easier to use energy units based on the Stefan-Boltzmann relationship E=5.67e-8*(Tkevlin)^4.  So the value of the MBL would be 306.9Wm-2.

Below 271.25K water would turn to ice and water vapor would decrease to nearly negligible amounts.  Above water would be mainly in liquid phase with water vapor in the atmosphere based on the temperature and pressure.  Using the sea level barometric pressure simplifies calculations, so the liquid surface temperature would determine the profile of the MBL.  As shown, the equatorial temperatures are warmer which would increase moisture in the atmosphere expanding the MBL vertically.  Temperature decreases with altitude AND heat content.  Moist air contains much more energy which takes longer to dissipate, so the altitude of the MBL increases with the energy content of the moist air.  The width of the MBL also varies with the total amount of moist energy which means the total volume of the MBL varies with total moist heat content.

By using an "average" temperature of the ocean surface  and relating that to the fixed value of the MBL a simple energy flow relationship can be obtained.  With the "average" sea surface temperature (SST) being approximately 294.25K degrees with an equivalent energy of 425Wm-2 and the MBL energy of 306.9Wm-2, there would be a steady state energy flow of 425-306.9=118.1Wm-2.  This is THE average total energy flow from the sea surface to the MBL.  This is way too simple a concept for most geniuses to grasp.

So by defining the Moisture Boundary Layer one can start at the most relevant thermodynamic frame of reference in the complex climate system of Earth.  It does help knowing what TOTAL energy means in terms of a steady state flux.  By multiplying this steady state flux times the total surface area of the MBL, one can get the big ass number they are looking for to impress their friends.  Then if someone just wants to solve the problem, they can stick with the stead state energy flux between boundary layers and not mess with the big numbers until the end :)

On the drawing above is a red band with a small oval noted as CBL, the Conductive Boundary Layer.  With the average SST energy of 425Wm-2 and the flow of 118.1Wm-2 to the MBL, the maximum energy of the surface at the CBL would be 425+118.1=543.1Wm-2.  For the degree K fans, that would be a temperature of 312.9K or 39.07C degrees.  This is well below the boiling point of water.  If the MBL was the only limit of energy flow, that would be the maximum SST.  With the Earth in some conditional state of equilibrium, meaning we are here to discuss this subject, there would be another limit or the oceans would continue to gain energy until there is no ice to provide a sink of the heat internally.  Kaboom is a word that comes to mind.

Since the energy of the MBL is 306.9Wm-2 and the steady state energy flow to this boundary is 118.1Wm-2, there would be a second Radiant Boundary Layer (RBL) that would have an energy of 306.9-118.1=188.8Wm-2.  Why would this layer exist?  If the MBL is stable as in conditional equilibrium and receiving 118.1Wm-2 of energy it would also have to rejected 118.1 Wm-2 of energy to maintain the 306.9Wm-2 of energy fixed by the freezing point of salt water.  That gives us a conditional equilibrium value for the RBL of 188.8Wm-2 with a temperature for the degree K fans of 240.2K or -33C degrees.  Conversely, the average maximum SST energy would be 306.9+188.8=405.7Wm-2 which the degree K fans would figure out is 305.8K or 32.6C degrees at equilibrium.

Looking at the opening figure, one should notice that the MBL does not enclose the entire surface of the Earth.  If it did, the kaboom word would be useful.  To not go Kaboom, the internal flows of energy would have to be in a steady state as well.  Electically, this would be a parallel circuit internal to the system.

With the flow to the Radiant Boundary Layer at 188.8Wm-2 and the flow to the MBL at 118.1Wm-2 for this conditional equilibrium condition, the internal flow from equator to ice the same over some period of time.  That caveat needs to be added because there is a 1.9C difference between the freezing point of salt water and fresh water.  For now it is easy to stick with the salt water temperature and energy reference so let's stick with easy and say the moist air flow is the same to the poles as it is to the MBL, which is kinda the point of defining the MBL, simplicity.

There will be heat flow in the liquid water of the oceans though that does not have the luxury of picking the path of least resistance.  In order to estimate this internal flow, the enthalpy of water has to be considered. In order to change the temperature of one gram of water one degree C, it required 4.2Joules of energy be transferred.  To be consistent, Wm-2 would be nice.  Joules per second and Watts per second are conveniently identical.  A cubic meter of water contains 1000 kilograms of water and there are 1000 grams per kilogram.  That means there are 1,000,000 grams of water per cubic meter.  If we think of a cubic meter as a stack of 1,000,000 grams of water then we can have 1 gram equivalent of water per face of the cubic meter.  In other words, 4.2Wm-2 per second in water is equal to 4.2 Joules per second, tah dah!  The average temperature of the SST is 294.25K and the freezing point of salt water is 271.25K which is a temperature difference of 23K degrees.  To change water 23 K degrees requires 4.2Wm-2 per degree equaling 96.6Wm-2 of internal average energy flux for a salt water sink.  The freezing point of fresh ice is 1.9 C warmer, which would be 4.2*21.1=88.6Wm-2.  This energy flux does not include phase change and would likely not include any significant radiant heat transfer.  This is energy flux is most likely simple thermal diffusion, aka sensible heat transfer.  The  use of the term "most likely" is intentional.  There would be some phase change from ice to water and back at the MBL and the amount of salt and other impurities in the water would change the thermal conductivity of the water.  This will provide an interesting challenge.

In this drawing the 425Wm-2 average is used with the optional sink energies for the range of salt to fresh dominate conditions.  The deep ocean sink would be lower, 2.75C degrees for salt dominate and 4.4C for fresh dominate, for this conditional equilibrium state.  Under salt dominate conditions, more energy would be absorbed in the deep oceans which would increase the energy of the system causing the MBL envelope to expand.  That expansion would include more fresh ice which negatively feeds back on the internal heat content by raising the freezing temperature at the MBL.  So with this range of potential feed backs, it would likely be better to build the model based on the average.  Interestingly, this guarantees the model will be incorrect, but would make it more useful for determining the impact of the feed backs.

By using (306.9+315.6)/2=311.25Wm-2 for the MBL reference, the model would look like this:

For the specified average ocean energy emission of 425Wm-2, the average MBL atmospheric energy emission would be 113.75Wm-2, the average ocean energy flux internally to the sink temperature would be 92.6Wm-2, which would produce an absymal depth temperature of 3.6C with an inward energy flux of 92.6Wm-2.  which gives us a new flux to complete the balance.  331.5-311.25=20.5Wm-2 from the deep ocean depths to the polar ice regions, with, 113.75-92.9=21.15Wm-2 from the surface atmosphere to the polar ice region.  The difference, 21.15-20.5=0.65Wm-2 indicating either some error or there is another source of energy not considered, possibly, geothermal :)

The range possible from fresh dominate to salt dominate regimes, should span the glacial and inter glacial climates.  That story will be left for another day.

Variation in the Moisture Envelope and Expanding the Model

The moisture envelope, or the volume enclosed in the Moisture Boundary Layer varies seasonally.

In Northern hemisphere summer, the envelope shifts toward the northern pole.  Since the actual pole experiences temperatures above 0C degrees, moisture is a factor in the summer months, the envelope includes the entire polar region.   The Radiant Boundary envelope also includes the entire pole.  The tropical heat band of the oceans move northward.  However, since there is a greater percentage of land area, the higher energy portion of the SST averages closer to the Equator.

In Southern Hemisphere Summer, there is a more uniform poleward shift of the higher energy portion of the sea surface temperature, the overall volume of the moisture envelope increases as does the radiant envelope. Despite the higher solar insolation during SH summer, the radiant boundary of 240.2K does not fully include the southern polar region and the moisture boundary does not include the southern most polar region.  These differences provide a chance to tweak the basic model.

The chart above is the sea surface temperature and temperature of various atmospheric layers as determined by the AQUA satellite.  It shows that the oceans are warmer during the Southern Hemisphere Summer and the atmosphere is warmer during Northern Hemisphere Summer.  Since the model is based on SST and not surface air temperature, using the satellite data with the model should help reduce some of the uncertainty associated with the surface temperature record.  There will still be uncertainty, but designing the model for the satellite data should be an improvement.


UPDATE:

Using the modeled 118.1Wm-2 MBL energy flux with the AQUA SST and 188.8Wm-2 Total energy Flux with AQUA channel 6, the blue  and orange plot show the estimate energy imbalance.  The Yellow plot is AQUA ch-2 minus the 188.8Wm-2 reference and enlarged with the right Y axis indicating the mean imbalance for the period as approximately 0.24Wm-2 and the regression showing the imbalance approaching zero.  Note: this is only the estimated ocean imbalance enclosed in the Moisture Boundary Layer envelope.

The 240.2K Radiant Boundary Layer

By using the freezing point temperature of salt water and an estimated 50% relative humidity a Moisture Boundary Layer (MLB) can be defined to reduce the complexity of the energy budget of the Earth climate system.  If the temperatures inside that "envelope" are stable and the atmosphere beyond that envelop is stable, a conditional equilibrium with a steady state internal energy flux equal to the steady state energy loss through the MBL layer can be assumed.  That rate of energy flow is estimated at 118.1Wm-2.  Now we can define a new boundary layer.

By using the 118.1Wm-2 as a reference and 306.9Wm-2 for the MBL boundary we can set our new boundary layer at 306.9-118.1=188.8Wm-2.  For this layer to have that radiant energy flux, it would have a temperature of 240.2K degrees or about -32C degrees.  This is sufficiently low that there should be no significant water vapor at this temperature.


For the MBL to be in equilibrium with this outer boundary layer, there would need to be an equal source internal to the MBL to balance this energy.  Inside the MBL 294.25 was used as the Taverage which has an equivalent energy flux of 425Wm-2 or 118.1Wm-2 greater than the MBL shell.  To balance the 240.2K boundary layer at 188.8Wm-2, the Tmax inside of the MBL could be the value of the MBL shell 306.9Wm-2 plus 188.8Wm-2 or 495.7Wm-2.

The drawing shows the Moisture Boundary Layer contained inside the Radiant Boundary Layer with the core energy source required to maintain the radiant sink at equilibrium.  The latent heat of fusion of water is 334J/g and the latent heat of evaporation is 2257J/g both at sea level pressures. In side of the Radiant Boundary Layer all significant water phase changes would take place.  If water is to be conserved and energy to be conserved, then the total energy change in the freezing, melting or evaporation of water would take place inside of the Radiant Boundary Layer.  The volume enclosed in the Moisture Boundary Layer would change with the total energy available and the volume of ice outside of the MBL would vary proportional to the ratio 2257/334 = 6.76.  For each gram of water evaporated, 6.76 grams of ice would have to form if the system is to remain in equilibrium.  The volume of the MBL would expand or contract, but the energy flows at steady state would remain constant.

Those of you still awake may have noticed that the 306.9Wm-2 or 271.25K values of the MBL are based on the freezing temperature of salt water.  Fresh water has a higher freezing point at 273.15K, 0C which has a radiant energy of 315.6Wm-2.  Since the vast majority of liquid water on Earth is salt and the vast majority of frozen water is fresh, that would mean that conditions inside and outside of the MBL would vary depending of the ratio of salt water to fresh ice, that pesky 6.76 ratio that has to be considered.  So for completeness, there should be a 273.15K secondary boundary layer.

This drawing shows the boundary layers with the pesky ice and snow layer.  The enthalpy of fusion limits the temperature of the surfaces covered with fresh ice and snow to 0C at phase change.  If there is ice and the temperature is below 0C, the ice only has a sensible impact on energy flux.  At phase change though the ice would release or absorb 334J/g.  In order for the MBL to expand or contract the enthalpy of fusion would have to be considered.  ]

Now there are a few things interesting about the model so far.  With the MBL layer at a stable 306.9Wm-2 and the total average energy Earth's surface estimated at 390Wm-2, the land surface outside of the MBL would have to provide 390-306.9=83.1Wm-2.  Since the energy flux of the Radiant Boundary Layer is 188.8Wm-2, land surfaces inside of the RBL but outside of the MBL would have an average radiant energy or 188.8+83.1=271.9K degrees.  Some of those still awake may be running to their calculators right now :)


The next installment

Defining the Moisture Boundary Layer

The Moisture Boundary Layer is the region where water exists only as a liquid or a vapor.  Adding salt or other impurities changes the freezing point of water.  This causes the MBL to have a variable limit that would need to be considered depending on the more dominate quantity, fresh or salt water.

As the temperature of the water increases, more water would evaporate.  The volume enclosed in the MBL would vary with the average temperature and energy contained in the MBL.  Since the volume of water that air can contain varies with temperature, an assumption that air inside the MBL on average contains 50% of its maximum capacity can be made.

Minimum temperature and humidity of the moisture boundary layer

On the psychrometric chart above is the defined lower for the moisture boundary layer based on the freezing point of salt water and 50% relative humidity.  The vertical line from -1.9C (271.25K) stops at the 50% RH curve.  The horizontal line is the sensible heating/cooling process where there would be no change in the moisture content of the air, only the relative humidity.

Moisture Boundary with average heat loop

Since we have an approximate Taverage, the average sea surface temperature of 294.25 K (21.1C) degrees and are using 50% RH as a baseline, the red line indicates the rise in moisture content for the high energy portion of the moisture cycle.  The blue line is the combined sensible and latent cooling from that maximum.  The low temperature end of the loop is not closed at this point since the chart does not consider the heat of fusion.  From the average energy point, the enthalpy of the air is approximately 41Joules per gram of dry air and the lowest point approximately 2 Joules per gram of dry air a difference of approximately 39J/g.

The sensible heat is equal to the specific heat capacity of the air time the change in temperature, for our atmosphere at sea level the specific heat of dry air is approximately 1 J/g at  sea level and the difference in temperature is 21.1-(-1.9)=23C.  The change in enthalpy, 39J/g is the total change in capacity resulting in a sensible heat ratio of 23/39=0.59 for the loop.

Using the Stefan-Boltzmann relationship, 294.25K has an energy of 425Wm-2, 271.25 has an energy of 306.9Wm-2.   There is a difference of 118.1Wm-2 which would be a steady state flow if the MBL was not changing or in equilibrium.  With a sensible heat ratio of 0.59, 0.59*118.1=69.6Wm-2 would be the sensible portion of the heat loss inside the MBL.  With the MBL radiating energy at a rate of 306.9 Wm-2 and it is receiving an average of 425Wm-2 from the interior, to remain in equilibrium it would have to radiate 118.1 Wm-2, the difference in the energy levels.  The internal energy flux of the MBL would be equal to the energy flux lost to the atmosphere beyond the MBL.  Assuming there is negligible water vapor beyond the MBL  118.1Wm-2 transferred through the MBL would be all sensible heat.  118.1-69.6=48.5Wm-2 may be purely radiant or a combination of conductive, convective and radiant.

Energy would also be transferred in the liquid water.  From 294.25K to 271.25K there is the 23C change in temperature, it requires 4.2J/g of energy to change water 1 degree C, that energy would be 4.2*23=96.6J/gram which would be 96.6Wm-2 per second by definition.

None of these rates of flows consider the total flow inside or outside the envelope of the Moisture Boundary layer.  They do provide some insight on the best way to proceed.

1. 96.6Wm-2 is a conductive flow rate within the water.  That would have a slower rate of flow than in the less dense atmosphere.

2. 118.1 Wm-2 is the approximate flow rate in the atmosphere from the average ocean surface temperature to the 271.25K lower temperature limit of the MBL.  This rate of flow is higher indicating that it would be more likely to determine the steady state conditions than the internal ocean flow rate.

3.  The psychometric chart estimate using the 50% relative humidity base indicates a Sensible Heat Ratio (SHR) of 0.59 and an approximate total enthalpy of 39J/g which can be used to estimate the to annual ice volume change for equilibrium conditions once total energy flows are estimated.

4. By defining the MBL lower limit as 271.25K and 50% relative humidity we can use conservation of energy for that thermal "envelop" to estimate the next thermal boundary layer which would have little to no latent heat, which should help simplify further calculations.

The next installment

Not So Fast

In the Slowing Down Series, which I will undoubtedly revisit to clarify points, I proposed a special case of condition equilibrium.  Because of the massive amount of water on Earth, the heat of fusion and evaporation provide a range of temperature controls allowing the surface not only to be warmer than the amount of absorbed energy would imply, but to allow the Earth to maintain a warmer range of temperature for a much wider range of available energy than previously imagined.

The heat of fusion of salt water is approximately 271.5K degrees.  In order to change phase from liquid to solid, the salt water much release more energy than require to just reduce the temperature one degree.   The temperature of the freezing point of salt water and the enormous mass of salt water provides for conditional equilibrium controlled by the steady state energy required to balance the heat released during fusion.

The heat of fusion of fresh water is 273.15K.  In order to change phase from solid to liquid, the fresh ice requires more energy be absorbed that just for the change of ice one degree.  The temperature of the thawing point of fresh ice and the amount of absorption required provides for a conditional equilibrium set point dependent on the total available mass of fresh ice.

Since the 271.5K set point is dependent on the huge total available mass of liquid salt water, it is the more stable of the two set points.  The 273.15K set point becomes dominate when the mass of fresh ice is sufficiently large.  Under this control condition, the radiant energy of the ice plus the heat of fusion energy released determines the average temperature of the Earth.  315.6Wm-2 plus 6.07J/gram of ice melt in a season.  Since the amount of energy provide to the Earth is limited by the Sun, the maximum energy available with current solar insolation is 1361.8Wm-2 which when divide by 4 to allow to the spherical shape of the Earth would be 368.08Wm-2.  368.08-315.6=52.4Wm-2 of energy released by fresh ice thawing for an average temperature of 283.8K or 12.53 C degrees as a conditional equilibrium temperature.  This condition would have the greatest albedo impact which would likely result in less stable temperature control.

For the 271.5K set point the conditional equilibrium using the same solar value would be 368.8-306.9=61.9Wm-2 of energy gain required at a stable temperature of 283.8K degrees.  With the albedo of liquid salt water being near zero, the system would easily exceed this requirement resulting in a higher average temperature.  Without albedo feedback, the upper temperature would be limited by the heat of evaporation.  Obviously, boiling would set a maximum temperature, but evaporated water would condense releasing the heat gained in evaporation imposing a limit below 100C.

The next step would be to narrow that range.

Slowing Down Part IV

Warning! This pushes the limits of every thermodynamic term or principle ever published.
The simple model of a steady state system in conditional equilibrium is pretty useful but a little bit limited because of the concerns of radiant versus other thermodynamic heat flows.  Since radiation has different spectra for different molecules and temperatures, it is somewhat more complicated.  Heat flow though is generally well understood since it is a vital part of so many aspects of life.  The resistance to heat flow or insulation value of a barrier can be describe in terms of R-value.  In SI units, R-value is in units meters square-K/Watts or simply degrees K/Wm-2. It is more often listed as degrees C, but degrees K are inter changeable.

With the heat of fusion of salt water as a lower limit and the 83.3Wm-2 established as the latent component of the system, we have part of the solution.  Using the increase in temperature at that temperature, 0.81C for 3.7Wm-2 we have a clue for the next step.  0.81/3.7=0.219 or the R-value associated with the internal system changes for the problem.  Since the resistance to energy flow from the system to ambient is the same, the R-value would be the same.  R-value is a general measure of heat flow and not specific to conductive, convective or radiant types of heat flow.  If we use the approximate initial conditions for the Earth, 288K and 390Wm-2 with the 271.5K 306.9Wm-2 determined with the simple model we can estimate an initial R-value.  (288-271.5)/(390-306.9)=. 16.5/83.1=0.198K/Wm-2.  This is slightly lower than the 0.219 estimate as it should be, but there is some uncertainty in how accurate both values are.  With Earth there is an external heat source, the sun which transfers some heat to the surface and some to the atmosphere with some reflected by both.  With the simple model we are only considering the internal balance to the external layer of the same temperature.  Since the internal energy calculation is based on the latent heat of fusion and evaporation, the R-value calculation would consider everything other than latent.  Convection, conduction and radiant combined would be equal to the latent heat transfer using this estimate.  That may be correct, perhaps not, but a reasonable initial estimate.  We need to start a new layer to find out.

306.9 is the new layer radiant energy.  The energy lost at the top of the atmosphere is estimated at 240Wm-2, the difference would be 66.9Wm-2.  This would be the total radiant heat flux from the 271.5K layer to space.  Using the initial R-value estimate 0.198*66.9=13.24K temperature drop from this layer to the next.  Using 0.219*66.9=14.65K temperature drop.  The difference 1.41K degrees would be the increase in temperature due to the 3.7Wm-2 of additional insulation.

This layer though is a transitional layer.  The 83.3Wm-2 of latent heat would transition to sensible heat which with the 66.9Wm-2 would total 150.2Wm-2.  0.198*150=29.7K temperature drop from the 271.5K layer or 241.8K degrees.  That would indicate a transitional layer from 241.8K to 258.3K for the initial conditions.  The final conditions would vary with the latent response and of course there is still uncertainty in the initial conditions.

Slowing Down Part III

With the basics of thermodynamic system in conditional equilibrium with steady state heat flow,it is easier to understand the somewhat complex responses to changes in the system.  With a lower sink flux limited by the latent heat of fusion, the upper source flux would be limited by the latent heat of evaporation or the the rate of evaporation, if there is sufficient differences in the energy of the two thermal masses.  If the heat of evaporation is not the limit, then the rate of evaporation would allow a range of temperatures for the source.

Carefully consider this special case of conditional equilibrium.  You have two or more objects in a steady state which is in equilibrium with another common steady state.  One steady state would be controlled by a phase change which maintains a stable temperature while there is sufficient matter to undergo that phase change.  That stable temperature maintains the second steady state condition with another object or ambient in this case.  Since the energy absorbed or released during phase change is much greater than that required to change temperature without a phase change, there would be a conditional equilibrium.

For a simple example consider the  freezing temperature of salt water, ~271.25K degrees.  The radiant energy of water at that temperature is 306.9 Wm-2.  With common insulation, the energy flow to this sink would be equal to the energy flow to the ambient sink, if the system was in equilibrium.  If the total energy flux of the the objects insulated from ambient is 390Wm-2, then the energy flux into the internal sink would be 390-306.9=83.13Wm-2 which would equal the rate of evaporation.  For fresh water the freezing point is 273.15K which would radiate 315.6Wm-2.  With an average energy under insulation of 390Wm-2, 390-315.6=74.4Wm-2.  With salt water freezing and fresh water melting, the rate of evaporation at the source would range from 83.13 to 74.4 Wm-2.  Both conditions are much greater than the heat loss or gain without a phase change.

 Relative to ambient, imposing a greater resistance to heat loss would increase the internal temperature until a new conditional equilibrium state is obtained.  Reducing the loss to ambient would reduce the transfer from the internal source to the internal sink by an equal amount if the system does return to steady state.  Since the internal sink temperature is 271.2K for freezing and 273.15K for melting, these temperatures would increase greater than the source.  A full 3.7Wm-2 impact at the 271.5K (306.9Wm-2) freezing point would increase that temperature to 272.06K, a 0.81C increase, for a 3.7Wm-2 increase in the resistance to heat flow.

Since the internal system will seek to return to a steady state with ambient, the effective ambient sink would also increase by 3.7Wm-2.  272.06K is still below the freezing point of fresh water, so there would be an increase in atmospheric freezing of water vapor.

Why would this be a valid conditional equilibrium?  The "stable" temperature varies.  Because energy cannot be created nor destroyed.  While the temperature may vary, the energy released during fusion would be the same as that gained during melting.  There would be a small shift in temperature requiring a small change in energy, but the net energy of the cycle would remain the same.

Based on this simple model with complex conditions, 3.7Wm-2 of additional "forcing" would produce 0.81C of average temperature increase with an increase in the rate of precipitation.  This model does not consider the individual radiant spectrum changes or potential chemical responses to the change in "forcing".  The model can be expanded.

Slowing Down Part II

Warning! this pushes the limits of every thermodynamic term and principle ever published.
Slowing down  was the first part of the basic of basics of a thermodynamic system in equilibrium with steady state energy flow.  It is not equilibrium or steady state, it is a combination where the equilibrium and steady state are conditional on each other, conditional equilibrium.  Determining the energy flux that is steady state is the simple part.

The highest energy determines part of the conditional equilibrium, the energy level of the largest thermal mass the other part. If the lower energy portion has a very large thermal mass relative to the higher energy portion, the duration of the internal conditional equilibrium would be limited by the thermal mass of the warmer object.  If the thermal mass of the two objects is equal and no energy is added to the system, the energy transfer from warm to cold would decrease to zero at the average energy of the two objects.  This case for no energy added to the system would produce the longest duration of conditional equilibrium.  If the thermal mass of both objects was infinite, there would be true equilibrium.  If less than infinite, then the energy flowing from the box would decay to the average energy content, then decay more slowly as the internal objects inside are in "true" equilibrium.  In a complex thermodynamic system there would never be a true equilibrium, only various conditional equilibria.  If fact, without a phase change a large enough mass to undergo the phase change, this special cause of conditional equilibrium could not exist.

When a phase change is involved, the temperature of the phase change would be maintained until the phase transition is complete.  The total energy required for a complete phase transition can be used to determine the slope of the decay to true equilibrium.

Example:  If heat of fusion of water is 4000J/kgK and if the energy flow from the warmer to colder is equal to 4000J/kgK, then the latent heat of fusion of water is controlling the internal steady state.  The temperature of the heat of fusion is 273.15K for fresh water, the temperature of the heat of fusion of salt water is 271.25K, in a salt water environment, the lower energy object effective radiant energy would vary between salt water freezing and fresher ice melting.

This is not your typical thermodynamic equilibrium.  In a complex non-linear thermodynamic system there would be no true equilibrium.  There would be a steady state maintained by the heat of fusion or by the heat of evaporation.  If you place a large block of ice in a perfectly insulated box, the temperature of the box would remain at the melting point of ice until all the ice were melted.  The steady state is conditional on the ability to maintain the phase change and the external equilibrium conditional interior maintaining a constant temperature.

Slowing Down Part III

Slowing Down

Warning!  This pushes the limits of every thermodynamic term and principle ever published.  I tend to leap ahead and skip steps I consider obvious.  That is not good for explaining things, but great for solving puzzles.  So let's take a step back and slow down.

If you have two objects in an insulated box that are in thermodynamic equilibrium with each other, they will be in thermodynamic equilibrium with the ambient conditions outside of the box.  If 50% of the objects are at one temperature or energy level higher than the rest, they determine the steady state condition of the thermodynamic equilibrium.  So if the energy flux from the warmer half  to the cooler half is 100Watts, the energy flow from the total of the interior to ambient will be 100Watts.  You can vary the percentages anyway you like, the warmer will still determine the steady state condition if the system is in equilibrium.  If you add insulation to the box, the energy flow from warmer to colder will increase proportionally to the decrease in energy flow to ambient until equilibrium between the interior objects is restored.

Why is that statement correct?  If the two objects are in thermodynamic equilibrium, removing the insulation would not change their equilibrium for a finite period of time.  If there was 100Wm-2 flowing from one to the other, there would still be 100Wm-2 flowing once the insulation is removed.  Removing the insulation would cause both objects to emit more energy elsewhere, but they would remain in equilibrium with each other.  The steady state flow rate would gradually decrease if they had large thermal mass, more quickly if they had small thermal mass, but the equilibrium would remain.  This is conditional equilibrium or equilibrium dependent on balanced steady state conditions.

The chart above is the sensitivity of that box to an addition of 3.7Wm-2 of additional insulation equivalent.  The higher the highest temperature, the lower the impact.

Slowing Down Part II

Why is the Sensitivity 0.8 Degrees

UPDATE:  Fishing accomplished



I started this blog because I was posting climate stuff on my energy blog.  The reason for the climate stuff was that alternate energy was becoming less of a hot topic.  A shame, because there is some very interesting alternate energy options out there.  When I started looking at the climate science, I noticed some things that just did not fit.  Global warming is just one big ass thermodynamics problem.  Thermodynamics involves a lot more than just infrared radiation.

The first thing I noticed is that the term down welling long wave radiation is used.  DWLR is nothing more than the temperature of the sky which can be used as an indication of the resistance to outgoing infrared radiation.  Pretty much anyone that has ever insulated something knows that radiant heat loss is an issue, but conductive heat loss also has to be considered.  If you insulate a wall with a dry, still air space it will lose less heat.  Most don't know that if you add a radiant barrier, it will lose 1/3 less heat.  A complete radiant barrier increases the resistance to energy flow by 50% meaning it is responsible for 1/3 of the energy savings.  2/3rds of the heat loss would still be due to conductive initiated energy flow.  Radiant barriers do not stop conduction so there is not perfect insulation or combination of insulation types.  There will always be heat loss, you can only reduce the amount.

Since heat loss is a given, you can figure out about how efficient your insulation may be, by seeing how much adding some more would change things.  To do that, you need to know where you are first.  The Earth has an average of 240Wm-2 of heat loss.  The average surface temperature is around 15 degree centigrade, so the interior heat is around 390Wm-2 on average.  The difference between what is retain and what is lost is 240Wm-2 minus150Wm-2 equaling 90Wm-2.  Since space is at near zero degrees absolute, that difference seemed a little higher than it should be.  About the most heat that out atmosphere should be able to retain should be half of the 150Wm-2 or 75Wm-2.

The reason it is higher is because the upper atmosphere also can gain and lose heat.  Since we have more heat retained, there must be a lower surface energy sink.  The coldest region inside the atmosphere is the tropopause.  It has a temperature that varies, but since the Earth is retaining more energy than it should, the tropopause should have a temperature that radiates 75Wm-2 which is about -82.5 degrees C.

While there are dozens of ways to estimate what flows should balance what temperatures in equilibrium, the Earth is not a simple box, it is a complex dynamic system.   Still there are some ways to simplify.

With the thought experiment there are 10 objects inside the insulation.  Seven are radiating 425Wm-2.  They represent the oceans with an average temperature of 294 K degrees.  Three are radiating at 308Wm-2 representing the land areas at 271.5 K degrees.  These are close to the average temperatures currently.  Note that 271.5K is just a little below freezing, roughly at the freezing point of salt water.  The latent heat of fusion of the masses of sea ice buffer the lower temperature.  While the system is dynamical complex, the freezing point of water, adjusted for the salt content, stabilizes the lower temperature range.  Since there is a large seasonal change in solar radiation, the sea ice rebuilds each winter.

The difference in the energy of the water and land mass on average produces an average flux from warmer to colder.  Since these two surface are enclosed in a common insulating blanket, the energy flow out from the combined masses is equal to the flow from the warmer oceans to the cooler land, which is 117Wm-2.  Since the total energy of the interior is 390Wm-2 with 117Wm-2 instead of 240Wm-2 at the top of the atmosphere, the difference would the radiant energy of the sink for the heat from the interior.  240-117=123Wm-2 This energy level is equivalent to the average tropopause temperature of -57.2 C which has an energy of 123Wm-2.

The sensitivity to an additional restriction to energy loss of 3.7Wm-2, the approximate forcing associated with a doubling of CO2 would vary base on the local energy.  By taking the ratio of the forcing 3.7Wm-2 and the surface energy flux at any reasonable temperature, this chart provides estimates of the sensitivity.

The curve intersects 288K, the average surface temperature around 1.0, 294K the average ocean temperature around 0.9 and decreases as temperature rises to approximately 0.8 at 305K or 32 C degrees, the high average temperature of the tropical oceans.  That sensitivity, 0.8C would be the approximate no feedback climate sensitivity to 3.7Wm-2 forcing by any cause.  The higher the ocean temperature in the tropics increases, the lower that sensitivity will become.

Proving why will require more work, but a simple model can produce interesting results.

Forgive any typos, but fishing comes before proofing.

BACK FROM CATCHING:  So if you have read this far you see some numbers but nothing that blows any wind up your skirt.  It really should.  The 271.5K average temperature of the land mass portion happens to be the freezing point of salt water within a small margin of error.  As salt water freezes, it has to release more heat, the latent heat of fusion, providing a feedback to the atmosphere.  With the enormous volume of water on Earth, this provides a long term feedback, on the order of  thousands of years.  When the Salt water freezes it forms fresh ice.  The melting point of fresh ice is 273.15 K degrees or about 1.65 C warmer which would limit the radiant heat gain set point by 7.56Wm-2.  So during an inter glacial period, there would be less fresh ice, the controlling temperature would be closer to 271.5K and during a glacial period, the controlling temperature would be closer to 273.15K.  That greatly limits the variation in "Average" Earth temperature.  Since the overall feedback is negative, as in sensitivity increases with decreasing temperature, this tends to erase the "faint sun" paradox and plays hell with the Green House Gas theory.

It also would pose some problems with ice core proxy reconstructions.  In the Antarctic where temperatures never exceed 273.15K degrees, the results would be totally different than in the Arctic where some eras the ice would never thaw and other eras where the surface layer of the ice could thaw.  Depending on the amount of thaw, the gases trapped in the ancient ice would not represent the conditions when the ice was deposited, but the conditions where the surface ice layer thawed.

Now you can have a long laugh at this outlandish claim, but I am afraid there are a few errors in Climate Science that are significant.