Thermodynamic Reference Layers - A Visual Aid

When discussing the Greenhouse Effect, radiant energy tends to dominate the discussion and most folks have  some difficulty visualizing some of the concepts.  This visual aid will not be perfect, but hopefully, will resolve some of the problems.  The numbers in Watts per meter squared correspond to temperatures if each of the colored layers were ideal radiant surfaces.  Radiant energy emits isotropically, or in all directions equally.  Since the drawing is in two dimensions you have to imagine that each of the colored layers are emitting towards, away, up, down and to each side.  The arrows for the red 500 Wm-2 point to what would be the poles of the Earth.  From the Equator, the center of the red, temperature drops by about one degree for each degree as you get closer to the points of the arrows.  316Wm-2 is the energy of a surface at 0 degrees Celsius, the freezing point of fresh water.  240Wm-2 is about -18 C degrees which is what the temperature of the Earth looks like from space.  200 Wm-2, about -30 C degrees (28.4 C actually, but 30 is a nice round number) is approximately the effective radiant layer of the atmosphere and 65 Wm-2 is roughly the effective temperature of the tropopause, which may require some explanation.

Since the coldest temperature ever measured in the Antarctic is about -90 C degree (~65Wm-2)  it is a good reference temperature in my opinion.  In my opinion just means it is an assumption, there is no known physical property that restricts the tropopause to any fixed temperature.  The -30 C degrees is an approximation based on the Stephens energy budget estimates which tend to make reasonable sense.  The 240 Wm-2, -18 C is used often in the literature as the no greenhouse gas temperature of the surface of the Earth based on what it would appear to be from space.  The freezing point of water is a solid physical standard.  Even the freezing point of water can vary, so all these layers are just rough references.

Below the red layer is supposed to be the deep oceans.  334Wm-2 is roughly the radiant energy of a surface at 4 C degrees, the approximate average temperature of the oceans.  The oceans though are liquid and much denser than the atmosphere.  Because of the density of the characteristics of liquid water, radiant energy is not typically used in liquid energy flow calculations.  Water has a density of about 1 kilogram per liter at sea level.  Air has a density of roughly 1 kilogram per meter cubed.  Since there are 1000 liters in a cubic meter, the density of air at sea level is about 1/1000 of the density of water.  As altitude increases, the density of the air decreases which causes a great deal of the confusion.  Density and heat capacity are related.  Lower density, lower heat capacity.

As density decreases, the utility of radiant energy transfer makes more sense.  There is less conduction and convective energy transfer because there are few molecules to collide with each other transfer energy by contact, conduction.  Since convection is driven by differences in density, the lower the density the less difference there can be, so convection decreases.  The only means to transfer energy in a vacuum is through radiant energy.

The effective radiant layer of 200 Wm-2 is at an average altitude of about 7 kilometers but if you live near the poles you know that it can be -30C (-22F) in your backyard in the winter and even in the summer if you vacation in the Antarctic.  Adding CO2 to the atmosphere will cause a shift in that layer by about 3.7Wm-2 per doubling of CO2.  Since temperature and effective radiant energy are related by the Stefan-Boltzmann relationship, the new temperature at a doubling would be about [(200+3.7)/5.67E-8]^.25 or 243.7K or about 1.1C warmer.  The average radiant layer near the poles would move by about 120 kilometers.  Since the density of the atmosphere at about 7 kilometers is less, the effective radiant layer would rise by about  100 meters.

This drawing is the same with vertical "Walls" inserted at roughly the freezing point of water, 0C 316 Wm-2. Since there is a temperature difference across those walls, energy would flow from the warmer portion to the the colder polar regions.  Since air has a lower density than water, the 4C, 334 Wm-2 region of the oceans extends beyond the approximate 0 C air wall.  In discussions of the Greenhouse Effect, the Earth is modeled as a flat disc with only the up/down portion of energy transfer used for simplicity.  If the oceans and atmosphere had a uniform density or if the Earth were uniformly heated, there would be nothing wrong with that simple model.  However, the real world is not as simple.  The internal energy flow has to be considered to determine the ultimate impact of a doubling of CO2.  With the approximate temperature and energy of the Effective Radiant Layer being -30C and 200Wm-2 and using the rough 4C 334 Wm-2 of average ocean temperature with that much larger energy density, 334-200 or 134 Wm-2 is a reasonable estimate of the energy flow one would expect through the "Walls" at the higher latitudes of the Earth.  Since the solar energy that determines the 240Wm-2 layer is assumed to be constant, even though it is highly variable with respect to 3.7Wm-2 of CO2 "forcing", the location of the vertical walls with ~134Wm-2 passing through can expand or contract with internal changes in heat capacity which increases with density.  As density increases, the role of conductive and convective (advective if heat flow is not vertical) increases.

Since the Earth is a sphere, the area impacted by an increase in total heat capacity decreases as the walls expand toward the poles.  The decrease in area and heat capacity, there is less mass to heat, would have to cause a shift in energy flow by increasing the average altitude of the poleward Effective Radiant Layers or by increasing the rate of energy flow into a warming higher density surface.  At some point, the conductive and convective means of energy transfer would limit the degree of warming possible since the area available to absorb the additional energy decreases with the increase in total energy.

To add to the complexity, the heat capacity of the northern "wall area" is less than the southern "wall area".  In order to transfer energy internally, conduction or advection in the form of ocean currents would have to transfer energy through or below the higher temperature tropical surface and atmospheric temperatures, the 500Wm-2 red zone.  The rate of that conductive and convective (advective) heat transfer is extremely slow, on the order of thousands of years, much like the variation in temperatures indicated for the past million of years in the paleoclimate reconstructions.  Global average surface temperature depends on the efficiency of internal heat transfer dominated by conductive and convective (advective) transfer.

Diurnal Temperature Ranges

This will be another work in progress.  Diurnal temperature range (DTR) should decrease with water vapor feedback, but there are several things that complicate using DTR for proving or disproving anything.  The first is that the change is small and the accuracy of the data likely not all that great.  Siting issues that may impact surface station readings would be as much or more a problem with the DTR.  So far, the Tmin data provided by the Berkely Earth Surface Temperature (BEST) project looks pretty good, but the further back in time you go there are major issues and not using anomalies, that would be amplified.

Using the BEST Tmax and Tmin, the chart above compares the northern and southern hemispheres.  The more current data shows a shift, but the older data is eerily consistent.  Not what one would expect, but since the data is averaged over an area with few stations in the past included in that average, the few stations likely don't allow for the resolution required.

The two charts above, the Galapagos Islands and Iceland are areas of prime concern since the ocean heat capacity change would be the major influence on each.  Iceland shows a major shift in 1985 and the Galapagos a shift of a different kind to greater variability.  That could pose a challenge.

 Canada has a reverse issue where the number of surface stations decreased in the newer data.

Comparing Canada DTR minus Russia DTR with the North America DTR minus Russia DTR, there is a similar dip in the mid 60s early 70s, so expanding the region should allow some gut check.

Doing a overlay of North America DTR with Asia DTR, the 60s-70s dip also would be noticeable and the 1985 shift is obvious.

That 1985 shift is likely due to the southern ocean shift that can be seen in the GISS LOTI regional data.  

 The shift is in the 44-64S Antarctic Circumpolar region and not obvious to some.  The upper chart shows the trend from 1900 over the other regional data on a 1980 to 2011 baseline.  The 0.007 C trend is 0.7 C per century with a R squared stat.  In the second chart on the 1980 to 2011 period is used showing zero trend and zero R square stat.  A zero trend would show a zero R squared stat, but the 0.856 R-squared for only a 0.007 trend is pretty spiffy.

So as I wade through the BEST data sans R programming, I will try to flesh this out a little more.  However, that will not be a big priority since I am sure this stuff must have attracted some attention elsewhere.

Oceans and Averages

The Mass of the Oceans is about 1.4x10^21 kilograms.  Since there are 1000 grams per kilogram, that would be about 1.4X10^24 grams of salt water.  The energy stored in a gram of salt water (~35g/kg) at 4 C degree is about 16 Joules.  That would make the approximate total energy contained in the world's oceans about 2.2X10^25 Joules if the true average temperature of the oceans is ~4 C and the average salinity ~35g/kg.

The approximate total area of the World's oceans is 361 X 10^6 km Squared with an average depth of about 3794 meters.  Since there are 1000 meters per kilometer and 10^6 meters squared per kilometer squared, the approximate area of the World's oceans is 361X10^12 m^2.  A layer of the ocean one meter deep and covering the entire World oceans would contain 361X10^12 meters cubed.  Since there are 1000 kilograms per cubic meter and 1000 grams per kilogram, a one meter deep surface layer of the
World oceans would contain 361x10^18 grams.  With the average temperature of that one meter deep surface layer of the World's oceans between 17 and 21 degrees C,  and there being ~4 Joules per gram per degree C, the average energy contained in the one meter surface layer of the World's oceans would be between 2.4X10^22 Joules to 3.0X10^22 Joules.

If we consider the top 100 meters of the World's oceans to be the "mixing" layer, then the average energy contained in the 100m deep mixing layer of the World's oceans would be 2.4 to 3.0 X10^24 Joules if the average temperature of that 100 meter deep mixing layer is between 17 and 21 C degrees.

Since 1955, it is estimated that the total heat content of the World's oceans have increased by approximately 14X10^22 to 25x10^22 Joules.  If all of that energy increase was limited to just the 100 meter "mixing" layer, that layer's heat content would increase from approximately 2.414 to 3.25 X10^24 Joules.

The 25X10^22 Joule increase in the heat content of the 0 to 2000 meter depth of the World's oceans, a little more than half of the total depth of the World's oceans, is two orders of magnitude lower (1/100th) than the total heat capacity of the World's oceans, if the average temperature is 4 C and the average salinity is 35g/kg.

Since the "pause that refocuses" in surface temperature, that huge 14X10^22 to 25X10^22 Joules or global ocean heat uptake since 1955 is the refocus of many in the climate debate.


Now if the average Surface temperature of the World's oceans is 17 C degrees, which would be 290 K degrees which has a Stefan-Boltzman equivalent energy of 400Wm-2 which is equal 400 Joules per second.


The Berkeley Earth Surface Temperature project estimates the 1951 to 1980 absolute land surface temperature to be 8.93 C or 282 K degrees with an S-B equivalent of 288Wm-2.  Since the total area of land surface is 146X10^12 m^2 of the 510X10^12 m^2 of the World's surface, if the Best average is correct for land and the 17C is correct for the oceans, the average surface temperature of the World would be ~287.6K degrees.  If the 21C degrees is correct for the average temperature of the World's oceans is correct, the average surface temperature of the World would be ~290.5 K degrees.

With the approximate average surface temperature of the World between 287.6 and 290.5 K degrees, the approximate average surface energy flux would be between 388 and 404 Wm-2 or an average of 396 Wm-2.

Just trying to organize some thoughts.

What's Time to a Planet?

More than half of the surface and energy of the planet Earth lies between latitude 45N and 45S.  The Northern Hemisphere has 70% of the land surface area and the Pacific Ocean is much large than the Atlantic Ocean.  Energy absorbed migrates in order to find some equalization, not a true equilibrium, at different time scales.  If there is more energy in the Southern Hemisphere than "normal" or more energy in the Pacific Ocean than :normal", climate would not be "normal".

If you don't know what "normal" is, you cannot make any claims what so ever as to what impact any change in any climate variable will have on climate relative to ":normal"  You would be shooting in the dark talking gibberish.

One of the more popular gibberish Faux Facts propagated by the warm and fuzzy climate pseudo-scientists is the X integrates to Zero.  Implying that X can be ignored.  That allows the pseudo-scientists to focus on their pet theory.  There is absolutely nothing wrong with "assuming" the X integrates to Zero, if you can confirm that X integrates to Zero in a reasonable time frame.  What are the time frames for the Xs?

This is where the pseudo-scientific discussions get to be amusing.  One will say that during the Pliocene, that CO2 was X and Temperature was Y, since Y is greater than today, the X caused Y so we can expect Y today.  Fine.  What else was different during the Pliocene and would that have an impact?

During the Pliocene, continents were likely close to their current locations, but there could have been about 250 kilometers drift from then to now.  The gap between North America and South America likely closed and that would imply that the gap between Antarctica and South America grew wider.  Currently, that gap is about 700 kilometers, so during the Pliocene that gap could have been 450 kilometers, or 64% less than today.  There is roughly 130 million cubic meters per second of water flowing through that gap today and could have been less than 83 million cubic meters per second of water flowing through that gap during the Pliocene.  Since the Gulf Stream current is about 30 million cubic meters of water per second today, having the impact of possibly two less Gulf Streams flows, might impact the rate that "global" energy redistributed.

So does the pseudo-scientists mention that?  Typically no, they do mention the closure of the Panama gap, but not so much the expansion of the Drake Passage gap.  Is that selective memory or selective science?

It seems that the new up and coming scientists don't share the same selective memory of the aging scientists trying to make their mark on humanity by saving the World from itself.  The new gang happens to notice that something just don't fit the models of the aging scientific super heroes.  That is how science progresses.  You look for gaps in theories and in this case, gaps between continents, the say, "How long did that take?"  After all, what is time to a planet?

Back Radiation - More of the Same Non-Sense

With the new Stevens and gang Earth Energy Budget comes the same non-nonsensical discussion of back radiation.  The 10 ball drawing above will be yet another attempt to stop that non-sense.

Between latitude 45N and 45S 70% of the surface of the globe, 73% of the surface of the ocean and about 90% of the solar energy available for the Earth can be found.  Not considering albedo, the average available energy can be as high as 612 Wm-2.  With 1361 Wm-2 "average" solar energy available at the mystical top of the atmosphere (TOA), 1/4 or about 340 Wm-2 would be the global "average" peak available energy provided by the Sun.  Between latitudes 45 and the poles, the amount of solar energy available, not considering the Earth's axial tilt, would decrease rapidly to zero at the poles.

The 612 Wm-2 is a "peak" value for the diurnal average it would also be the Day time average since at night the Sun doesn't provide energy.  Since the Earth rotates on its axis, this "peak" is just like the "peak" voltage of a sinusoidal power supply.  The root mean squared (RMS) value of a 612Wm-2 sinusoidal power supply would be 612 divided by the square root of two - 612/1.414=432 Wm-2.

Since 432 Wm-2 RMS is applied to 70% of the surface, 0.7*432=302 Wm-2 of the 340Wm-2 global "peak" is available in the 45N to 45S section of the Earth.  Just like a battery or capacitor, the Earth can "charge" to any value up to the "peak" depending on the discharge resistance, with "peak" being 612Wm-2 not the RMS value.

For some odd reason, this simple analogy to a well know electric circuit function is lost in the "Back Radiation" non-sense.  If I charge a battery, I do not attempt to determine the "back radiation" or back capacitance or back resistance of the surroundings of the battery case.  All that is required is the capacity of the battery and the resistances, plural, of the battery and the circuit it is connected to.

Resistances is plural because a battery can charge and discharge at different rates.  Internally, the battery's resistance to charging increases as it approaches its maximum capacity.  The circuit or load that the battery is connected to can vary with "demand".  If the demand is constant, then as the capacity of the battery reduces, the electromotive force or voltage reduces which would reduce the current or energy flow to the load or "demand".  Since the Earth's oceans have the highest heat/energy capacity, the charging resistance and load resistance would determine the condition of the Earth's Charge or average heat content.

By comparing the surface average energy available to the average voltage drop of the "demand" or surface temperature, you are comparing apples to oranges.  The surface temperature or "Back Radiation" if you use the energy equivalent of that temperature, is just an indication of the current flowing through the atmosphere.

Since the composition of the lower atmosphere includes much greater mass and more water vapor, the resistance to energy flow would naturally decrease with altitude.  In the denser lower atmosphere, energy is "conducted" by more than radiant means, so it is easy to confuse "back radiation" an indication of energy flow, with the actual energy capacity of the atmosphere the energy is flowing through.

If you consider the atmosphere to be another battery, you can determine its "charge" by subtracting the EMF of that battery from the total "back radiation" or equivalent "voltage" drop across its charging "resistor".  In the Stevens and gang Earth Energy Budget cartoon, the All-sky Long Wave absorption is 188Wm-2 and the surface EMF is 398Wm-2,  398-188=210Wm-2 is the surface energy flowing through the atmosphere and 188 is the average "charge" of the atmosphere as a result of the true Earth surface battery.  Since 210 is flowing through creating the 188, 22 Wm-2 would be the voltage drop of the atmosphere or the "back radiation" felt at the "true" surface generated by energy flow from the surface to the atmosphere.

The Atmosphere has a alternate "charging" mechanism.  It absorbs 75Wm-2 from the Sun.  That adds to the "voltage" of the atmosphere and some portion of the "voltage" would be felt at the "true" surface.  Since the resistance of the atmosphere decreases with altitude, how much of that 75 Wm-2 of energy is felt at the surface would depend on where in the atmosphere that 75 Wm-2 is absorbed.  If it is absorbed perfectly in middle of the energy concentration of the atmosphere, just like a voltage divider, 1/2 of the energy would be felt at the surface.  That would be 37.5 Wm-2 which would be felt in addition to the 22 Wm-2 created by the flow of energy through the atmosphere from the surface.  22+37.5=59.5Wm-2 would be the approximate "net" impact of the resistance on the atmosphere plus solar energy absorbed in the atmosphere or the "net" "back radiation" felt at the surface.

Since Stevens and gang indicate that the "net back radiation" is 53 Wm-2 (by subtracting 345.6 Wm-2 DWLR from 398 Wm-2 OLR), the atmospheric voltage divider may have slightly different resistances.

There is nothing wrong with using the gross values of radiant energies, but without considering the source of the gross energies and the methods of energy transfer, it is easy to confuse cause and effect.  That is why most "Sane" people avoid gross radiant values in systems that are likely not primarily radiantly driven.  If the water in one end of my pool is 10 C degrees and the water in the other end is 20 C degrees, I would not attempt to determine the average energy of the pool by converting 10 C to 283.15K, convert that to 365Wm-2 then determine that 20C has an energy equivalent of 419Wm-2 then use the gross radiant energy values to determine anything about a virtually radiantless energy transfer process in a frigging swimming pool.
 
I hope this helped.

Closer Look at Stephens and Gang Budget

Edit to correct the spelling of Stephens

Since I torn into Trenberth and Keilh's Earth Energy Balance, It is only fair that I tear into the Stephens' and gang Earth Energy Balance.  Stephens though does include realistic margins of error, so it will not be as easy.

Here is the biggest test, what does the atmosphere absorb?  Like K&T, Stephens and gang lumps outgoing long wave and down welling long wave together requiring some thought.  398 minus 345 rounded for simplicity is 53 Wm-2, the net outgoing long wave radiation absorbed by the atmosphere.  Solar, Sensible and Latent with this 53 OLR absorbed total 240 Wm-2.  That is approximately the net solar absorbed, notice that 20 Wm-2 all-sky atmospheric window passes through the atmosphere.  The surface absorbs 165 Wm-2 directly from the sun.  If you consider that the atmosphere is a radiant layer, ~ 1/2 of the 240 would be returned to the surface as "active energy" which would equalize at some point in time with the total 240 felt at the surface.  The 240 plus 165 equals 405 less the 20 Wm-2 through the atmospheric window would be 385Wm-2.  This is well within the error range of the Stephens and gang's graphic.

Note that OLR absorbed is 22% of the total absorbed by the atmosphere.  Increased CO2 would increase that value by 3.7 Wm-2 to 56.7 Wm-2.  Then the total absorbed by the atmosphere would be 243.7 and the surface energy would eventually increase from 385 to 388.7 Wm-2 with +/- 17 Wm-2 margin of error for the whole shebang.  That additional 3.7 Wm-2 would increase latent by ~ 3 Wm-2 cooling the surface but adding to the atmospheric absorption.  That could cancel most of the CO2 impact or add up to 3 Wm-2 to the impact producing 391.7 Wm-2 of surface energy( using my 385) at some point in the future.  The high end would be 6.7Wm-2 increase which at an average surface energy of 385Wm-2 would be roughly 1.24 degrees increase in average surface temperature.  That is below the minimum 1.5 Estimated by the IPCC and very close to the range estimated by several "skeptics". More warming that than would require feedbacks that are not evident so far.  That warming would also require warming of the oceans surface which would require warming to some depth in the oceans which requires an undermined time to fully equalize if it in fact could ever equalize.   So the estimated range of warming due to a doubling of CO2 is almost nada to 1.24 C degrees.  Not exactly the alarming number tossed about by climate activists.

Is Stephens and gang's Budget THE Budget?  I have no idea.  It does though more accurately resemble what climate has done of the past 40% of a doubling after considering other factors.

UPDATE 2:  Since I found another misspelling I may as well add this.  When I put in the separation, it is to simplify understanding of what is going where.  Trying to include both the day and night modes will always result in something that looks like it violates the laws of thermodynamics.  The budget cartoon is just that, a cartoon trying to get as much information as possible on one fairly simple drawing.  Someone noticed that the All-sky downwelling longrange is greater than it should be.  That is why I used the net and separated the atmosphere.  At night, the actually altitude of the source of DWLR would be lower than in the day and the amount of surface energy emitted would be less.  I estimated that night Fmin would be about 380Wm-2 and that day Fmax would be about 414Wm-2.  So the 240 Wm-2 I use in the split would be a rough 24 hour average with somewhere in the ballpark of 33Wm-2 variation on an annual daily average.  Like a said before, there Stephens and gang budget is not perfect, but a lot better than all the past budgets I have seen.

The New Stephens Cartoon

Graeme Stephens and company have a new paper in Nature Geoscience, that contains the above new and improved Earth Energy Budget cartoon.  All both of you that follow my ramblings know that I have had quite a few issues with past Earth Energy Budget cartoons that were not only wrong, but deceptively wrong.  Propaganda comes to mind.

Graeme a crew have a clue.  This cartoon is even better than the Bjorn Stevens and Steven Schwartz Cartoon I have mentioned on occasion  First let me highlight a major point in the above, -187.9 +/- 12.5 Wm-2 All-Sky Longwave Absorption.   With the average energy of the surface of the Earth being ~ 398 Wm-2, the -187.9 Wm-2 would have an equivalent energy of about 210 Wm-2 or an equivalent "surface" temperature of 246.7 degrees Kelvin which is -26.4 C degrees.  The effective radiant temperature of the atmosphere is -26.4 C  with a range from -30 to -23 C degrees approximately.  A doubling of CO2 is supposed to change that average temperature by about 1.5 C degrees.

If you were to imagine a band of constant temperature between -23 and -30 C degrees in the atmosphere, you would noticed that at certain times of the year, that band would disappear below the surface of the Earth.  Adding CO2 would move where that band penetrated the surface closer to the poles or higher in the mountains by whatever distance it would be 1.5 C degrees cold than it is now.  As you get closer to the poles, the percentage of surface there is, that would be impacted by the 1.5 C degree reduction gets smaller until at 90 degrees South or North there is no longer any surface to be impacted.

If you consider energy, the 1.5 C degrees is roughly 3.7 Wm-2.  That increase in energy has a decreased impact on temperature as the surface to be impacted warms.  At the equator, 3.7 Wm-2 added to a surface at 500 Wm-2 would have 3.7/503.7=0.069 or a 0.7 percent impact on temperature.   Instead of the surface temperature at that spot on the equator being 33.3 C it would be about 33.8 C or about one half of a degree warmer.  The average warming in the inhabited regions of the Earth would be about 0.67 C degrees or less.  UNLESS, there is significant positive feedback.

Since that amount of no feedback warming at the "true" surface of the Earth is less than the uncertainty in the "average" "surface" temperature of the Earth associated with an energy of 398 Wm-2 +/- 5 Wm-2, discussing short term initial impacts of a doubling is like arguing over the number of angels that can do the Polka on a pin head.  Basically, only pinheads would even attempt to discuss initial impacts of small changes in CO2 forcing in face of the over whelming uncertainty.  For a pinhead to confidently state that warming due to CO2 doubling will be between 1.5 and 4.5 C degrees at a 95% confidence level is ludicrousness squared.

Charging Mushy

While Joseph R. Genius, PhD is off on a lecture tour, Uri F Kidding publishes in an obscure journal the Mushy Charging Theory.  After determining that if any energy absorbed below the "surface" of Mushy that is not completely released prior to the next Mushy noon, that Mushy will continue to internally warm, the good Dr. Kidding used a "Battery" analogy.

A battery being charge from a full discharge state has an internal resistance of nearly zero.  At full charge with a constant electromotive force, the internal resistance of the battery is nearly infinite.  The battery charges at a rate proportional to the applied electromotive force time exponential of the capacity of the battery and the resistance of the battery.

The electromotive force (EMF), the Sun, provides a peak energy of 1361 Wm-2 in a sinusoidal pattern with a period of ~24 hours.  With a peak value of 1361 Wm-2, the RMS value of the solar force would be 1361/(2)^0.5 or 962Wm-2.  Since Mushy is a sphere, the resistance to energy loss would decrease toward the poles.  If that resistance were regular, the effective EMF would be ~ 578Wm-2 or the average of distribution across the peak longitudinal band excluding albedo.

Since the albedo of Mushy is not 1, then some energy will penetrate the "surface" and the RMS value of that energy would be the "charging" current for the Mushy battery.  The final value at and "Surface" would depend on the initial "trickle charge rate" and the cumulative charge capacity of each layer or cell in the Mushy battery.

 Mushy would absorb energy and the true "surface" energy would be greater than the average EMF applied to the surface by a factor of 1.414.  In other words, if 240 Wm-2 is the simple average applied, 339 Wm-2 would be the full charge value.  "Of course, the final "surface" energy would depend on the charging rate and capacities of each layer, which requires further funding for research." Uri F(n) Kidding

Mushy Ball Surfaces

Mushy Ball is the new fictitious planet in solar orbit.  Since Mushy is new to the neighborhood, no one is sure what will happen with Mushy now that the light of day is shining on the planet.  Professor Joseph R. Genius believes that the planet will turn into a frozen rock.  Professor Uri F. Kidding thinks J.R. is smoking something and that Mushy will turn into an Earth like planet.

Uri whips out his simple model showing that at Mushy noon, the new planet has exactly the same solar forcing as Earth at the "surface" and that IF Mushy absorbs 25% of the energy below that surface it would have nearly the exact same energy absorption that the Earth has.  Junior responds that Mushy is still cold and with freeze creating a pristine white snow covered surface that reflects 99 percent of the solar energy and to boot would emit 99 percent of any energy that was absorbed.

Uri shows the above chart and tries to explain time to Junior.  The chart is wall energy transfer.  The equator of Mushy receives nearly 960 Wm-2 of energy.  For Mushy to turn into a snowball, all of the energy would have to dissipate from the surface and sub-surface by the next dawn.  For that to happen, virtually no energy could be absorbed below the "surface" Junior sees, because the internal rate of energy transfer would not be the same as the "surface" rate of energy transfer.  Junior's theory has run into a wall.

The green curve is sub surface "Mushy" energy.  Whatever energy is absorbed at the equator, a portion of that energy will travel towards the poles.  The curve shows the potential difference between 10 degree "walls"  Since the "surface" of Mushy is less dense than the sub-surface, the rate of transfer through these walls would be slower below the "surface" than above the "surface".

What Uri is trying to explain to Junior is that there is no "surface" but a series of surfaces.  Each surface, because of different density of composition would have different internal and external rates of energy transfer.

Surface 1 would have wall transfer 1.  Each progressive surface in the chart above absorbs half the energy of the surface before.  The wings of the first wall are taller, so it would be easier to transfer energy to the surface than to the poles.  The deeper the absorption penetrates  the easier the energy trans fer to the pole is with respect to the surface.  Since surface 1 absorbs 25% of the incident radiation, surface 2 is 12.5%, surface 3 is 6.75% and surface 3 is 3.375% of the full radiant energy at the equatorial surface.  If the "surface" is frozen away from the equator, the transfer of energy becomes more difficult and the "surfaces" below the frozen surface retain more energy.  For Mushy to not gain energy, the equatorial surface would have to be impenetrable.   With the sub-surfaces retaining more energy, even if is only a fraction of a Watt per day, Mushy will approach Earth like stored energy conditions.

Mushy Ball

Imagine, if you will, a mushy ball orbiting our Sun.  All we know about the new mushy ball is that it reflects some light, 30% to be exact.  While we can't be sure, the mushy ball seems to have a temperature.  Since we know the mushy ball's distance from the Sun and how much light it reflects, we can estimate that is should have a surface temperature, if a mushy ball has a surface, of about 255K degrees +/- a couple.

Joseph R. Genius, a renown scientist with the University of Psychedelic Experimentation determines that the mushy ball must have an interesting phenomena if it has a surface temperature greater than  255K +/- a couple.  So J. R. Genius determines the total surface area of the mushy ball without bothering to determine if the mushy ball has a surface and proclaims that Mushy has a "surface" area of  4*pi*r^2 and that only half is illuminated, 2*pi*r^2 , but the actual area that is being shown upon is that of a flat disc, pi*r^2, so the average energy that impacts the surface is pi*r^2/4*pi*r^2 or 1/4 of the energy shown on a flat disc evenly distributed across the entire mushy surface.

Uri F. Kidding, also a renown scientist, says, "Okay Junior but what is the surface and why are you assuming uniform distribution of the energy?  If Mushy is absorbing energy, that energy would tend to have a gradient from the warm equator to the colder poles."

"Because that is what S. R. Genius proposed in the peer reviewed literature."


And there you have it, the complete story of global warming.  If planet Mushy can be constructed of any material and still have a "Greenhouse effect" then Jr. got some "splainin' to do.

 "For the record I intuitively feel something is not right at a very fundamental level."  Feelings are not science, but there is something in that simple comment lifted off a popular climate blog.  Planet mushy is likely the key.  

The Simple Radiant Model ( see here, here and here if curious) uses a simple cosine function.  Latitudinal internal energy transfer would penetrate "walls".  If the area of the "walls" are equal, then the transfer is simple.  If the "walls" restrict transfer, then that complicates the situation.  Since the radius of the Earth is ~6371 kilometers, a parallel cross-section of the Earth would be pi*[6371*cos(latitude)]^2.  If the temperature or energy of the smalerl section is greater than the larger, energy would flow easily.  If the temperature or energy of the larger section is greater, then there is a choke or bottle neck for energy flow.  In equilibrium, the energy at any point would be balanced by the energy of all surrounding points.  Since the Earth is not in true equilibrium, but a pseudo-steady state, then the energy flux from a point would have equal resistance to flow in all directions.  Energy would be uniformly distributed and maintain that uniform distribution based on the resistance at each surrounding point.  

Neither is the case with Earth, but planet Mushy can be forced to play that game.  First, we have to straighten Mushy's axis, can't have that season variation between hemispheres.  Now let's look at the latitude 60.  That is where the cosine is 0.5 so the wall at 60 degree latitude would be 1/2 the area of the wall at the equator.  The energy flowing from the equator through the 60 degree wall would be 1/2 the average value of the energy between 60N and 60S.  If any energy is absorbed into the surface of Mushy, since the surface between 60N and 60S gains more energy than the latitudes outside 60N and 60S there will be energy flow through this 60 degree wall.  If Mushy is in steady state and "conditionally" in equilibrium with the poles, i.e. 50% of the energy absorbed is flowing equally to the polar sections, the energy of the equatorial system would be in balance so that some percentage of the energy flow would be toward space and an equal amount of energy would be transferred to each pole.  Energy flow would be equally distributed, internally and externally. 

With this condition the energy flow through the equatorial wall would be zero, some percentage of the energy from 60S to the equator would be to space and some percentage into the 60S to pole section.  

Internal transfer of energy would look something like this.  Since Mushy is in a "conditional" equilibrium, both hemispheres have equal energy and both are losing equal amounts of energy to space.    At the equator, the "wall" energy transfer is zero.  The wall energy transfer peaks at 60 degrees latitude and at the poles, the mean internal energy transfer is lost to space.  So as long as Mushy absorbs any energy it would have to transfer energy internally, UNLESS, the energy was equally distributed both internally and at the "surface".    What Junior has to do is determine the mean "wall" transfer before Junior can determine the mean radiant impact, so he can determine the impact of any other changes to Mushy.

Now this considers the "walls" to be full cross sections.  If the depth of the walls vary with latitude we would have a different shape to the curves.  If the energy is unequally distributed we would have a different shape to the curves.  So without any change in the "forcing" or energy provided, the physical internal composition of Mushy and the distribution of Mushy's energy would impact energy transfer.  Unforced variability.

For temperature fans and as a double check, this the the temperature by latitude that the simple radiant model believes should be.  70% of 1361 Wm-2 is applied and distributed by the cosine of latitude.  The "peak" temperature is equal to 4th root of the energy by latitude divided by the Stefan-Boltzmann constant 5.67e-8 minus 273.15 for conversion to C degrees, day is divided by two and average is just the simple average by latitude.  The average for each is indicated in the legend.  The simple model is not perfect, but -14.2 C is the temperature it believes is appropriate for a no greenhouse gas Earth.  Since the Earth is a sphere, not a cylinder, this is a little higher than the simple average of -18C used in most cases.

The main point of the graph is between latitudes 45 and 65 where the Day and average values cross zero C degrees.  Mushy, regardless of its composition would absorb considerable energy in the middle latitudes and up to roughly 70 degrees could be above zero degrees with 70% of the available solar energy of 1361Wm-2.  If it takes longer than 12 hours for that absorbed energy to be transferred to the "surface" and then to space, Mushy would have a temperature greater than 255K +/- a couple.  

One of the big caveats of course is albedo.  If you assume Mushy is made of water than can be frozen, then the reflectivity would be higher, possibly as high as pure driven snow or it could be more interesting like, Mushy Ice, hence the name Mushy.

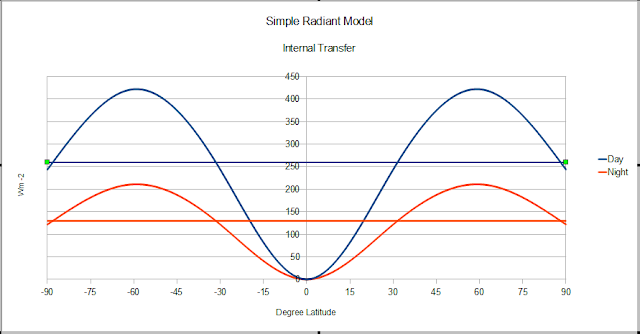
Just thought I would add this view of 10 degree walls.