Stefan-Boltzmann and the Green House Effect

I was really going to hold off on this until I had a little better punchline, but since I have already tossed out the ridiculously simple, Ein=Eout+dS-dW I may as well show some of my cards.  Correction: It is S, Entropy and W, Work, not the changes.

The Stefan-Boltzman law is a brilliant derivation of the energy of a two dimensional flat plate showing that the energy radiated is proportional to the absolute temperature of the flat plate object by J=alpha*sigma*T^4, where the sigma is equal to 5.67e-8 or the Stefan-Boltzmann constant.  The alpha is the curious adjustment required to make objects of varying thermodynamic properties proportional to true black bodies or that flat plate in the derivation.  Since any geometric shape can be approximated as a collection of flat plates, the S-B law, applied to nearly all object with this little caveat, "the object cannot re-absorb its own emitted energy."

From the Thermodynamic derivative, "It follows from classical electrodynamics that the radiation pressure 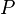 is related to the internal energy density:" P=u/3, where u is the internal energy.  


This little caveat has interesting implications.  The internal energy of water is not linear.  That energy is normally expressed as enthalpy.  So for the S-B equation to perfectly apply to water it would need to be based on the absolute enthalpy not the absolute temperature of the water.

For example: the specific heat of water at 4C is 4.205 Joules per gram.  At 32C the specific heat is 4.178 Joules per gram.  Very small difference but 4.178/4.205=0.9935 is the ratio of the change in specific heat.  So instead of 1 which would be a perfect black body we have 0.9935, close enough for most engineering work.  So just looking at the surface of water at 32C we would need a small correction for the emissivity which is better than the standard 0.924 approximation used for more exact estimates of distant objects with the S-B equation.

Where absolute enthalpy comes into play is that the internal energy of the object has to be transferred to the surface of the object, if not the value 0.9935 has to change.  Using the radiation pressure analogy, the enthalpic pressure would be the sum of the specific heats from the average internal energy or enthaply density to the surface.  That would be 121.3 Joules per gram from 4C degrees to 32C degrees.  The 4C temperature of water is pretty special.  It is the temperature of maximum density of pure water and its S-B equivalent energy is approximately equal to the energy of fusion, 334.5 Wm-2 versus 334 Joules/gram.  This would appear to indicate that the surface emissivity is indeed proportional to the internal Enthaply of the system.

Indications and verification are two different critters, but that is the direction I am moving in at present, defining the Absolute Enthaply in a form comparable to radiative pressure.  Kinda fun!